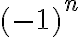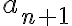Buenas, quería saber si el método dado en clase es válido en todos los casos, porque si analizamos la imagen que adjunto debajo podemos ver que se cumple que es decreciente, pero en realidad no lo es, porque si vemos la gráfica no es monótona.
Muchas gracias. Saludos.
Hola María, el método funciona siempre. Y, efectivamente, la sucesión que tenés es como se muestra en la gráfica, no creciente ni decreciente. El problema es que hay un error en los pasos de la demostración.
El error está cada vez que tachaste el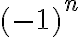 
en ambos lados de la inecuación (una vez en la demostración de que no es creciente y otra en la que intentas probar que es decreciente). No olvidemos que lo de tachar a ambos lados es una forma abreviada de dividir a ambos lados de la inecuación por el mismo número (en este caso, 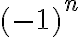). Pero al multiplicar/dividir por un negativo la desigualdad se invierte, cosa que no ocurre si el factor es positivo. Como 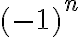tiene signo que depende de la paridad de 
, no podemos tacharlo así sin más.
Qué significa esto? Que la relación entre 
y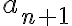 
no es siempre la misma (o sea, la sucesión no es monótona), y mirando un poco mas finamente, el crecimiento/decrecimiento se alterna según la paridad de .
Saludos
Genial, pensé que podría haber sido por algo de eso sí.
Muchas gracias. Saludos!