No logro comprender como probar que la función es biyectiva, creo que no entiendo como definen la función S a partir de un producto de matrices.
Hola Salvador, fijate que si haces el producto de matrices que dan la función \( S: \mathbb{R}^2 \to \mathbb{R}^2 \) resulta \( S((x,y)^t)=(y,x)^t \), y de esa manera queda definida, siendo geométricamente una simetría respecto a la recta x=y (como un espejo puesto a 45º).
Una función es biyectiva si es inyectiva y biyectiva a la vez:
Inyectiva: 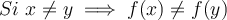 (o sino,
(o sino, 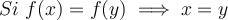 ). O sea que cada punto tiene una imagen distinta.
). O sea que cada punto tiene una imagen distinta.
Sobreyectiva: 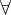 punto del codominio
punto del codominio 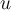 , existe un punto en el dominio
, existe un punto en el dominio 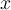 tal que
tal que 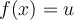 . O sea que todos los puntos del codominio son imagen de algún punto del dominio.
. O sea que todos los puntos del codominio son imagen de algún punto del dominio.
Estas son las definiciones de inyectivo y sobreyectivo y eso lo que hay que probar.
Cuando una función es biyectiva, la correspondencia entre A y B es uno a uno y por lo tanto existe una única función \( g: B \to A \) que es la función inversa que se define de la siguiente forma: \( g(b)=a \) si y sólo si \( f(a)=b \).
Probá si con esto ahora sale y sino lo seguimos viendo.
Saludos
Entendí perfecto y creo que me salió todo bien, gracias
