Foro Práctico 6

Hola Federico, disculpa la demora en responder.

Sea $$r$$ la recta que querés hallar, $$A$$ el punto por el cual tiene que pasar, $$s$$ la recta que interseca y $$t$$ la recta a la que es ortogonal (una aclaración acá es que ortogonal no es lo mismo que perpendicular: Perpendicular es un caso particular de ortogonal en el cual además de que el ángulo de sus vectores directores es 90º, las rectas son secantes. Por lo tanto, en este caso solo nos hablan de la dirección de sus vectores directores).

Como $$r \perp t$$ y $$A \in r$$ sabemos que $$r$$ vive en un plano $$\pi$$ cuya normal es igual a la dirección de $$t$$, $$v_t$$, y pasa por el punto $$A$$. Luego como $$s$$ interseca a $$r \in \pi $$ sabemos que $$Q=r \cap s= \pi \cap s$$, hallando $$Q$$ conocemos dos puntos de $$r$$ y por lo tanto la podemos hallar: $$r: P=A+\lambda(A-Q)$$.

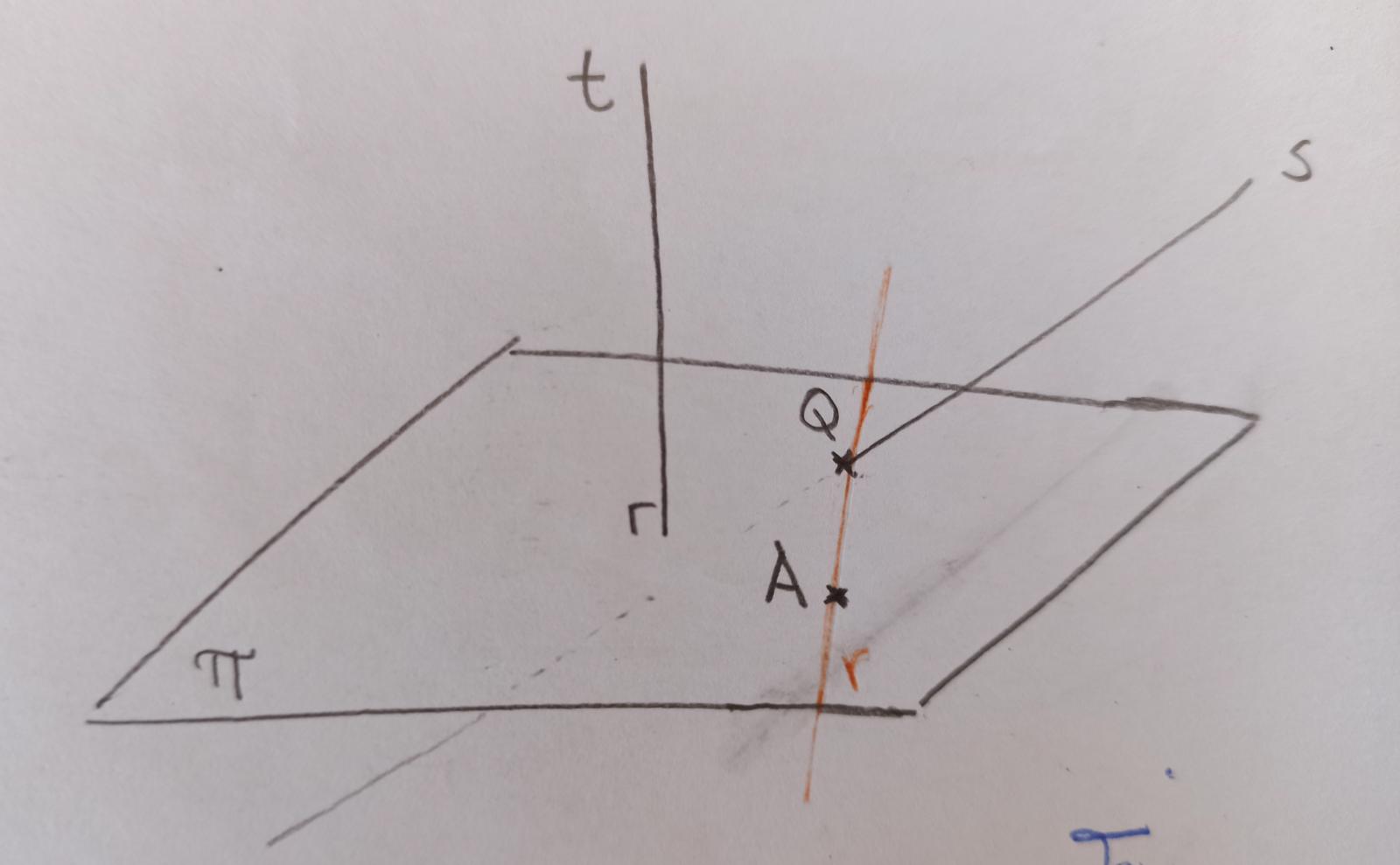
Si algo no se entiende preguntá de nuevo.

Saludos