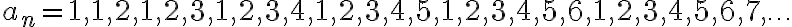Foro Práctico 3

Para construir una sucesiòn que aglomere en todos los naturales, podemos intentar copiar la idea de la sucesión de la parte anterior. Es decir, una sucesiòn que haga lo siguiente: recorrer los naturales de 1 a n, luego de 1 a n+1, y así sucesivamente, pasando por todos los naturales infinitas veces.

$a_n=1,1,2,1,2,3,1,2,3,4,1,2,3,4,5,1,2,3,4,5,6,1,2,3,4,5,6,7,\ldots$

Sin embargo, es un poco molesto escribir esto de forma compacta (a pesar de que la idea es correcta).

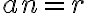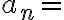Dado n, definimos $an = r$ si $n = p^r$ con $p$ algún  primo y $a_n=$ 0 en caso contrario.

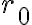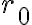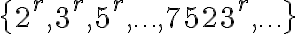Dado que los números primos son infinitos, y la descomposiciión de un natural en productos de primos es única, necesariamente $a_n$ deberá pasar por todos los naturales infinitas veces. Por ejemplo, dado $r_0$ natural, una subsucesión que converge a $r_0$ es la correspondiente a los números $\{2^ r , 3^ r , 5^ r , \ldots, 7523^r , \ldots \}$.