Hola María. Las raíces del polinomio característico no son totalmente obvias, pero se pueden hallar usando por ejemplo la fórmula de Bhaskara. Que en la solución aparezca dicho de un modo tan escueto es porque es un resumen de la prueba. Pero no son raíces inmediatas.
Dicho esto, te invito a observar que para hallar  y
y  no es realmente necesario pasar por el polinomio característico. Y tiene que ver con algo que está bueno tener en cuenta siempre que trabajamos con ecuaciones diferenciales: Si tenemos una función que sabemos (o suponemos, o queremos) que es solución, esta debe verificar la ecuación. En este ejercicio, justamente, nos dan una función que queremos que sea solución. Entonces un esquema posible de pasos para hallar
no es realmente necesario pasar por el polinomio característico. Y tiene que ver con algo que está bueno tener en cuenta siempre que trabajamos con ecuaciones diferenciales: Si tenemos una función que sabemos (o suponemos, o queremos) que es solución, esta debe verificar la ecuación. En este ejercicio, justamente, nos dan una función que queremos que sea solución. Entonces un esquema posible de pasos para hallar  y
y  es
es
- Tenemos 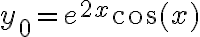 , que sabemos es solución. Derivo dos veces para hallar
, que sabemos es solución. Derivo dos veces para hallar 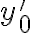 e
e 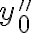
- Esas funciones halladas las sustituyo en la ecuación diferencial 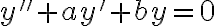 . En el miembro derecho vas a poder sacar
. En el miembro derecho vas a poder sacar 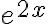 como factor común, y el otro factor va a tener algunos términos con factor
como factor común, y el otro factor va a tener algunos términos con factor 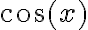 y otros con factor
y otros con factor 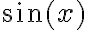 .
.
- Todo eso está igualado a 0. Y cuando decimos 0 acá nos estamos refiriendo a la función nula. No es el objetivo hallar un valor de  puntual sino que la igualdad valga para todo
puntual sino que la igualdad valga para todo  real. Esto sólo se logra si los coeficientes que multiplican a
real. Esto sólo se logra si los coeficientes que multiplican a 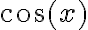 y
y 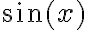 son ambos nulos. Y de ahí se pueden hallar
son ambos nulos. Y de ahí se pueden hallar  y
y  .
.
Fijate si se entiende esto y si te sirve para hallarlos.
