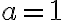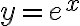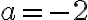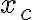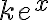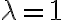Ejercicio 5

Ejercicio 5

de Agustin Silvano Garcia -
Número de respuestas: 4

Buenas, 

estoy resolviendo el ejercicio 5 y no estoy seguro si estoy por el camino correcto.


Lo que hice fue: 

  1. Obtener el polinomio característico de las ecuaciones para obtener los 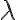\lambda  solución de cada uno de ellos.
  2. Analizar el discriminante de la solución según los posibles valores de a. Llegando a la conclusión que a < 1 para que ambas soluciones sean de la misma forma (raíces reales distintas).

No tengo muy claro como seguir, ¿debería igualar los 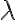 \lambda de cada uno de los polinomios para hallar el a resultado?


Gracias.


Saludos.


Agustín.
En respuesta a Agustin Silvano Garcia

Re: Ejercicio 5

de Alejandro Bellati -

Hola,


Ir discutiendo según el tipo de soluciones que tiene cada ecuación puede ser dificil, o no muy ordenado. Además, por qué ambas soluciones deben ser de la misma forma para tener una solución en común? Esto es falso, por ejemplo con a = 1 ambas ecuaciones tienen de solución y = e^x, cuando un polinomio tiene raíces dobles y el otro no. Entonces ir discutiendo según el tipo de soluciones puede ser molesto, justamente habría que considerar varios casos. Lo mejor, creo yo, es lo que se hace en las soluciones descartar el caso fácil ( a = -2) y observar que si se comparte una cierta solución en común x_c entonces restando ambas ecuaciones diferenciales se deduce que dicha solución es de la forma ke^x y por lo tanto \lambda = 1. Además esto se cumple si y sólo si \lambda = 1 ser solución de los polinomios característicos, no importa la multiplicidad.
En respuesta a Alejandro Bellati

Re: Ejercicio 5

de Julieta Perroni Solimano -
Hola, estaba resolviendo este ejercicio y llegue a la solución de la forma ke^x, pero no logro entender por qué de ahí deducimos que λ = 1.
Gracias.
En respuesta a Julieta Perroni Solimano

Re: Ejercicio 5

de Mateo Turqui Clark -
Hola Julieta,

Para este tipo de ec. dif. nosotros buscamos soluciones del tipo y(x) = Ke^λx, siendo λ una de las raíces del polinomio característico. Al llegar a la conclusión de que y(x)=e^x es solución en común de ambas ec. dif, entonces podemos comparar esto con la forma de las soluciones que buscamos (es decir: observar Ke^λx = Ke^x) y deducir que λ = 1, ya que e^x = e^1x.
Sabiendo que y(x) = e^x es solución común de ambas ec. dif., entonces podemos afirmar que los dos polinomios característicos ( Pc(λ) ) comparten raíz λ = 1. Esto quiere decir que ambos verifican que Pc(1) = 0, de donde finalmente podemos deducir que a = 1.