Foro Práctico 2

Hola Richard. Está bien sí. Aprovecho para hacer algunos comentarios sobre la escritura.

Si no me equivoco, esa constante $k$ surge de una exponencial con lo que en principio sería positiva (de hecho si no la igualdad de valores absolutos difícilmente se cumpla). Por otro lado y teniendo en cuenta lo dicho antes, la igualdad de valores absolutos puede reescribirse como

$y = +/- (x^2 - x)k, \forall k > 0.$

O bien, si admitimos $k$ negativo y contemplamos la solución constante 0 (veriicar que efectivamente lo es), nos evitamos el 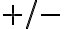$+/-$. Queda entonces

$y = (x^2 - x)k, \forall k \in \mathbb{R}.$

Por otro lado, fijate que vos mismo podés verificar si tus soluciones están bien. Una vez que tenés $y$, derivando obtenemos 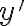$y'$ y podemos fijarnos si cumple la ecuación original o no.

En este caso 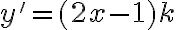$y' = (2x -1)k$, con lo que la ecuación original resulta

$x(x-1)(2x-1)k + (1-2x)(x^2 -x) = 0$

Que efectivamente se cumple para todo $x$, por lo que las funciones $y$ halladas son solución.