CDIVV-2S: Solución de la homogénea de una ecuación diferencial con raíces complejas

Buenas, tengo una duda cuando tengo por ejemplo la ecuación diferencial y''+y=0. Hallando sus raíces obtengo que una es i y la otra -i. Mi problema está en como debo plantear la solución homogénea, sé que es del estilo yh(x)=C*Cos(x)+K*Sen(x), pero me da incertidumbre saber si ese x que está dentro del coseno o del seno es positivo o negativo, según las clases de openfing depende del signo del valor que multiplica a i, pero no sabría con exactitud como es en realidad

Re: Solución de la homogénea de una ecuación diferencial con raíces complejas

de Veronica Rumbo - jueves, 27 de agosto de 2020, 12:57

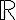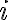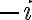Hola Ivan. El $x$ en cuestión puede ser cualquier valor de $\mathbb{R}$ . Con respecto al coeficiente que lo multiplica, es el mismo en ambos casos, ya que tus raíces son $i$ y $-i$ , y lo que nos interesa es el módulo 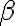$\beta$ de la parte imaginaria no su signo. O sea, en este caso la solución quedaría $y_H = C \cos(x) + K\sin(x)$ .

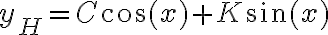Capaz te hace ruido pensar que, con el mismo criterio podría haber tomado el coeficiente 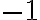$-1$ y escribir la solución como 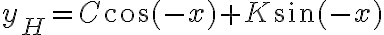$y_H = C \cos(-x) + K\sin(-x)$ . Y la respuesta es que sí, podría, y también está bien. Te invito a pensar por qué.

Re: Solución de la homogénea de una ecuación diferencial con raíces complejas

de Ivan Ezequiel Rivero Tabarez - jueves, 27 de agosto de 2020, 13:34

Bien, muchísimas gracias!!! Lo primero que se me viene a la cabeza es utilizar que coseno es par y seno es impar, pero me voy a sentar a pensar a ver que es lo que pasaría en realidad. Gracias!!