Buenas, mi duda era que cuando yo hallo los landa, como hago para hallar la solución general.
Gracias
Buenas, mi duda era que cuando yo hallo los landa, como hago para hallar la solución general.
Gracias
Hola Manel. Es importante recordar por qué estamos hallando las raíces de la ecuación caraterística (los 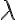 ).
).
Si tenemos una ecuación diferencial 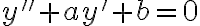 , con
, con  y
y  reales, sabemos que las soluciones son todas las funciones de la forma
reales, sabemos que las soluciones son todas las funciones de la forma 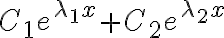 , siendo
, siendo 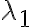 y
y 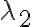 las raíces del polinomio
las raíces del polinomio 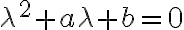 .
.
Es decir, hallamos los 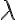 para poder hallar el conjunto solución. Recordemos que la solución en este caso es un espacio vectorial de dimensión 2.
para poder hallar el conjunto solución. Recordemos que la solución en este caso es un espacio vectorial de dimensión 2.
Saludos
Hola. La familia de soluciones es la misma, no importa cómo se llamen las constantes. Imaginate que las raíces del polinomio característico son 2 y 3. Entonces la familia de soluciones la escribo:
donde 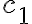 y
y 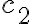 son constantes reales arbitrarias. Si vos escribiste tu solución como:
son constantes reales arbitrarias. Si vos escribiste tu solución como:
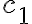 a lo que yo le llamo
a lo que yo le llamo 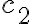 y viceversa. No importa el nombre, si hubieses escrito
y viceversa. No importa el nombre, si hubieses escrito 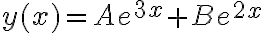 con
con  y
y  reales cualquiera, estás representando la misma familia de funciones.
reales cualquiera, estás representando la misma familia de funciones.