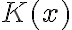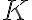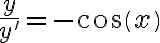Buenas, estaba mirando el video de resolución del ejercicio 3 del practico 2, y tengo una duda sobre el final. Cuando uno ya halló K(x), y eso lo pone en la ecuación y(x)= k(x).e^-sen(x), ésto en el caso específico de este ejercicio. El y(x) que nos queda, ¿Sería la solución general de la ecuación diferencial no homogénea, o simplemente es una solución particular?
Muchas gracias
Hola Leandro. No logré identificar el video pero asumo que estás refiriéndote a la parte a)1).
En el ejercicio 3 se pide hallar soluciones de ecuaciones diferenciales de primer orden, sin condición inicial, por lo que la solución no debería ser una función concreta sino una familia de funciones (un espacio vectorial de dimensión 1, para mayor precisión).
Lo que vos escribiste como 
es una constante 
arbitraria, que en este caso no hallaremos. Aparece al hallar la solución general de la ecuación 
, que es la misma pero despejada para resolver separando variables.
No sé si eso responde a tu duda. Como complemento te recomiendo mirar el ejemplo 2.3 de las notas:
https://eva.fing.edu.uy/mod/resource/view.php?id=116910
Que es muy similar a esa parte del ejercicio.
Saludos
Por ejemplo, en el b)1), la parte homogénea nos queda y(x)= e^(-sen(x)).K. Según entendí en lo dado en teórico, para resolver la ecuación no homogénea ahora tendría que tomar K como K(x), poner y(x) con esta forma nueva en la ecuación diferencial no homogénea y despejar K(x). Para luego volver a la ecuación y(x)=e^(-sen(x)).K, poner lo que nos dio de K(x) y de ahí saldría la solución. Lo que no se es si esta solución es una particular de la ecuación o sería la solución general.
Adjunto el video por si no quedo claro lo que quise plantear.
https://www.youtube.com/watch?v=DL2ZdSAmZeg&feature=youtu.be
Saludos
Hola.
La solución y(x)=e^(-sen(x)).K(x) = sen(x) - 1 que planteas es una solución particular.
Para conseguir la solución general es necesario considerar la suma de esta solución particular con las soluciones de la homogénea. En resumen, la solución general, o la familia de soluciones, es:
y(x) = C*exp(-sen(x)) + sen(x) - 1, donde C es una constante real cualquiera
Saludos