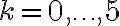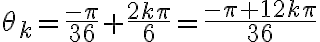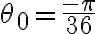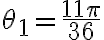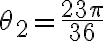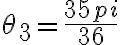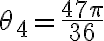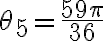Podrian subir por favor como quedarían los Z para los que se cumple. Ya que lo hice y me queda incoherente por los ángulos. Gracias
Caro me ganó de mano con la respuesta, estaba haciendo una applet para visualizarlo mejor así que aprovecho a dejarla a modo de complemento de su respuesta.
En ella podés ver, moviendo el deslizador, las 6 raíces buscadas.
- Obs: Puede confundir el Subíndice i (en la parte del módulo y el argumento de z) con la unidad imaginaria.
Guillermo muchas gracias por señal el abuso de notaciòn, ya lo arregle.
Mil gracias
Alguno podría explicarme como es que se llega a que el argumento es -π/36 + 2kπ/6
En primer lugar, observa que el argumento de 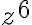 es
es 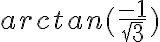 , que da
, que da 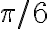 .
.
Luego, como al multiplicar complejos sus argumentos se suman, tenés que los argumentos de las raíces sextas que estás buscando deben ser tales que al multiplicarlos por 6 te de 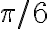 (o un ángulo equivalente, de lo cual sale el
(o un ángulo equivalente, de lo cual sale el 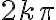 .
.
es decir, estás buscando argumentos 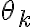 tales que
tales que 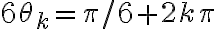 . Despejando, se deduce que
. Despejando, se deduce que 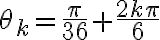

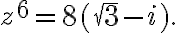
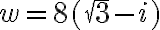
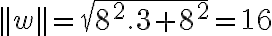
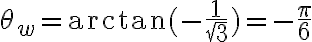
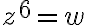

![||z_k||=\sqrt[6]{16}=2^{ \frac{2}{3}} ||z_k||=\sqrt[6]{16}=2^{ \frac{2}{3}}](https://eva.fing.edu.uy/filter/tex/pix.php/44a8a9d6ef65402739ec66cca680cdb0.gif)