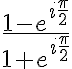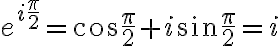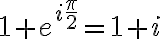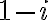Buenas! No me queda claro en este ejercicio que puedo hacer para lograr la notacion polar y asi hallar la binomica, trate de multiplicar por lo que vendria a ser el conjugado pero me queda una expresion rara. Alguna ayuda?
En el ejercicio tenes que escribir en forma binómica este complejo:
Es correcta la estrategía de multiplicar por el conjugado del denominador, para ello debemos hallar la forma binomial del mismo:
luego 
y su conjugado es por lo tanto 
.
Una consulta, no entendi completamente como continuar el ejercicio, luego que encontre la forma binominal de e^π/2i sustituyo y luego multiplico y divido por su conjugado o el conjugado que encontre lo multiplico y divido por la fraccion del inicio?
El objetivo sería "sacarnos de encima al denominador", digamos. Cuando digo eso, a lo que me refiero es a que el denominador sera un número real (así podés escribir todo en forma binomial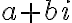 
donde en 
y 
quizás aparezca el denominador, pero es real así que todo bien).
Entonces para "eliminar" la parte imaginaria del denominador habría que multiplicarlo por su conjugado, en este caso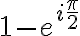 
o lo que es igual 
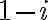. Y, obviamente, si multiplicamos por algo en el denominador, hay que hacerlo también en el numerador.
O sea que el paso a seguir para hallar la forma binomial sería multiplicar arriba y abajo por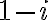 
y seguir operando.
Saludos.