Hola. ¿En el ejercicio 2.b esta bien escribir el conjunto solución de la forma que esta en la foto adjuntada?
En los ejercicios 3.a y 3.b, ¿puede ser que al final mi conjunto solución quede en función de dos variables?
En respuesta a Luciano Umpierrez Garcia
Re: Practico 1 ejercicios 2.b y 3.a y 3.b
de Bruno Dominguez -
Hola Luciano,
La forma correcta de expresarlo sería: \( S=\{(z,0,z,-z); z \in \mathbb{R} \} \), fijate que z=z entonces también que estar, además también tenes que indicar donde varía tu variable libre.
Un par de comentarios:
- Fijate que en la primer transformación elemental que haces, la calculas mal y luego arrastrás el error: 0 -3*(-1)=3. Corregí esto y fijate cómo te queda.
- Cuando estás resolviendo sistemas homogéneos no es necesario escribir la columna de los términos independientes, ya que esta columna siempre va a ser de ceros (si preferís escribirla xq te marea menos o lo que sea, podes hacerlo igual).
- No es necesario que hagas cada transformación elemental de forma independiente, x ejemplo las primeras dos las podrías haber hecho a la vez, ya que una no depende de la otra. Cuando hagas transf elem para lograr ceros en una misma columna, por lo general vas a poder hacerlas en simultaneo.
En el 3a sí te quedan dos variables libres (el sistema sería un SCI con dos grados de libertad), pero en el 3b no. Cualquier cosa preguntá de nuevo.
Saludos
En respuesta a Bruno Dominguez
Re: Practico 1 ejercicios 2.b y 3.a y 3.b
Gracias por la respuesta.
En el 3.a me quedó así como en la foto pero en el 3.b como se ve también me quedaron dos variables, podrías ayudarme?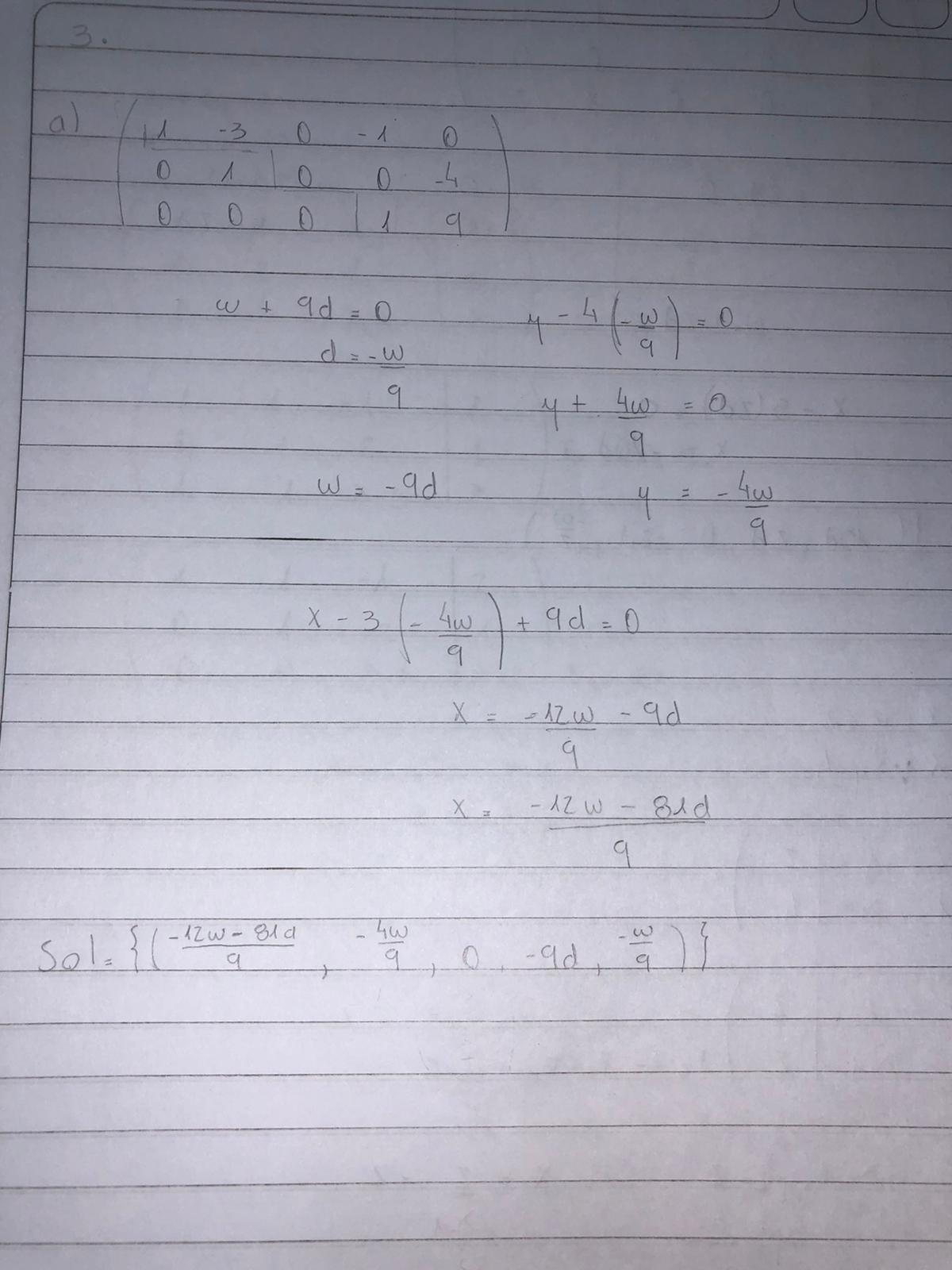 
En respuesta a Luciano Umpierrez Garcia
Re: Practico 1 ejercicios 2.b y 3.a y 3.b
de Bruno Dominguez -
Hola Luciano,
En el 3a:
- Primero un detalle, cuando dibujas la "escalera", se comes un número en la segunda fila y lo bajas después al "escalón", los cálculos después los haces bien igual.
- De forma general, aunque no tenes xq cumplirlo, se toma como variables libres las que forman el "escalón largo", en este caso d y z. Esto es a modo de automatización simplemente, a priori podes elegir cualquiera que no esté determinada como variable libre.
- Vos trabajaste con d y w como si no estuvieran relacionadas, pero como hiciste en tu primera cuenta sí lo están, por lo tanto no son dos variables independientes: \( w=-9d ; d \in \mathbb{R} \) como te lo planteo en el punto anterior o como hiciste la mayoría de las cuentas: \( d=-w/9; w \in \mathbb{R} \). Teniendo esto en cuenta, el valor de x te queda: \( x=-12w/9 -w = -7w/3 \)
- Luego como z no aparece en la ecuación significa que puedo tomar cualquier valor y por lo tanto es otra variable libre: \( z \in \mathbb{R} \)
Entonces la solución te queda: \( S= \{(-7w/3 , -4w/9 , z , w , -w/9) ; z,w \in \mathbb{R} \} \)
En el 3b:
- Te pasó algo similar que en el anterior w y d están relacionadas, por lo que en tu solución solo debe de estar una de ellas, si d es tu variable libre entoces d=d. Por lo tanto:
\( S= \{(-10d , 2d ,0, -2d ,d) ; d \in \mathbb{R} \} \)
Recordá poner en tu solución dónde viven (a dónde pertenecen) tus variables libres. Espero que haya quedado más claro, cualquier cosa preguntá de nuevo.
Saludos
En respuesta a Bruno Dominguez
Re: Practico 1 ejercicios 2.b y 3.a y 3.b
Muchas gracias, me quedo bastante claro. Saludos.
En respuesta a Luciano Umpierrez Garcia
Re: Practico 1 ejercicios 2.b y 3.a y 3.b
Yo lo hice, pero me quedó otra solución en ambos. 
En respuesta a Cintia Carina Cobucci Perrone
Re: Practico 1 ejercicios 2.b y 3.a y 3.b
de Bruno Dominguez -
Hola Cintia, el tema es que vos utilizaste otras variables para expresar a las demás. Por esto llegaste a otra solución, pero sigue siendo correcta. Un detalle en el a, tus variables libres son z y t, no z y w.
Saludos