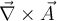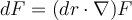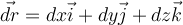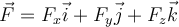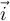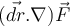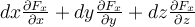Buenas, viendo el ejercicio 2 del practico 0 me surgió la duda de si el operador nabla cumple las siguientes propiedades 
Fabián,
No entiendo mucho tu pregunta, dado que algunas de las expresiones que planteas a priori no tienen sentido, o no me doy cuenta que tenes en mente.
Por ejemplo la expresión 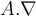 es extraña, dado que la derivada de
es extraña, dado que la derivada de  no estar'ia actuando sobre nada.
no estar'ia actuando sobre nada.
Las expresiones naturales son
Divergencia de un campo vectorial 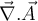
Laplaciano de un campo escalar 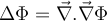
Tal vez puedas reformular tu pregunta en estos términos.
En todo caso no dudes en repreguntar.
Saludos
G
Dije gradiente pero quise poner divergencia. Mal yo
No. El operador nabla actúa hacia la derecha, por eso cuando estudiás la conmutatividad de nabla no puede cambiar el orden relativo del operador respecto al vector sobre el que actúa.
En particular en el caso que planteas, el operador nabla actúa sobre F, y no sobre el dr. O sea si
y
Análogamente para las componentes según 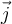 y según
y según 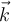 cambiando
cambiando 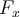 por
por 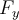 y
y 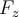 , respectivamente.
, respectivamente.