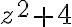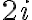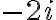Buenas,
Logre encontrar la solucion pero no me parece que sea la mejor manera de hacerlo. Lo que hice al principio fue cambiar z por bi ya que tenes el dato de que tiene al menos una raiz pura. Despues, iguale las partes reales e imaginarias a 0 y consegui que dos raices son 2i y -2i. Despues lo que hice fue encontrar un polinomio con estas raices como es z^2+4=0 y dividi el otro entre este.
Esto me dio como resultado otro polinomio que multiplicado por ese da el original. Le hice las raices y me dio 1+i y 1-i que estan bien, pero, hay alguna manera mas facil de hacer esto?