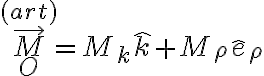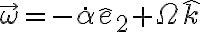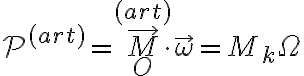Foro de consultas generales

Hola Leandro,

Si pensamos en el problema general (suponiendo $\alpha$ variable en el tiempo) de una barra (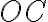$OC$) que se mueve en el plano especifiicado, necesitás algún mecanismo de sujeción que permita el giro libre en ese plano; una articulación cilíndrica lisa, cuyo eje sea perpendicular al plano vertical indicado, es el mecanismo adecuado (y por ser perpendicular a un plano vertical, debe ser horizontal).

Ahora, esa articulación no ejerce momento según su eje pero sí puede hacerlo en el plano perpendicular y vamos a considerar en ese plano (que es en definitiva el que contiene a la barra 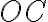$OC$) dos direcciones: la vertical, según la cual hay una velocidad angular impuesta 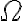$\Omega$ y una dirección más perpendicular tanto a la vertical como a la articulación en sí (usemos el versor 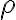$\rho$ de cilíndricas). El momento ejercido por la articulación lo escribo como:

$\vec M_O^{(art)}=M_k\hat k + M_\rho \hat e_\rho$

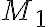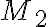y ahora voy a considerar el movimiento general del rígido (no puedo darte la idea del par motor con las condiciones mismas del ejercicio porque el momento de la articulación en sí da cero! Fijate que los $M_1$ y $M_3$ que nombrás son nulos y $M_2$ ya lo era por ser art. lisa):

$\vec \omega=-\dot \alpha \hat e_2+\Omega \hat k$,

donde incorporé la variación temporal de $\alpha$ a la velocidad angular. Si ahora hacemos el cálculo de la potencia como bien hiciste vos, nos queda:

$\mathcal{P}^{(art)}=\vec M_O^{(art)}\cdot\vec \omega=M_k\Omega$.

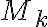Cuando está presente ($\alpha$ variable), $M_k$ es el responsable de aportar energía al sistema y por eso le llamamos par motor. En cambio, cuando está presente, 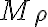$M_\rho$ no aporta energía pero evita que la barra se salga del plano (es lo que llamaríamos par reactivo nomás). Sin hacer el cálculo (podés intentarlo, claro!) te digo que cualquiera de los dos pares van con 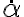$\dot \alpha$, por lo que desaparecen para el caso particular del planteo del ejercicio.

Saludos,

Ariel.