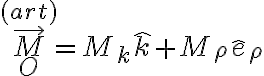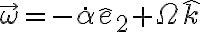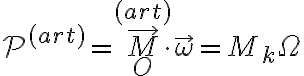MecNew: Examen diciembre 2015, ejercicio 3

Buenas. Iba muy bien con la resolución de este ejercicio hasta que me tranco en la parte b, pues consideraba que el momento de la articulación en O proyectado según 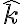$\hat{k}$ (versor vertical ascendente) es nulo, porque la articulación es cilíndrica lisa. Pero en la solución dice "para que 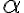$\alpha$ se mantenga constante" y proyecta la segunda cardinal según el versor \( \hat{e_2} \ sin incluir ningún término del momento de la articulación en O. Esto es exclusivamente porque 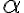$\alpha$ es constante? (si es así, no entiendo porqué) o tiene que ver con el hecho de que la articulación es cilíndrica lisa?. Para el planteo general no tuve problema, de hecho sin cuestionarme esto llego al mismo resultado que la solución, sólo que no entiendo la justificación de ese paso. Desde ya, muchas gracias.

Re: Examen diciembre 2015, ejercicio 3

de Ariel Fernández - sábado, 15 de agosto de 2020, 01:20

Hola Leandro,

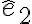la articulación que sostiene al rígido en $O$ es cilíndrica lisa de eje horizontal ( $\hat e_2$ según se nombra en la solución), por lo que al plantear la segunda cardinal al rígido desde $O$ y proyectarla según este eje, la articulación no contribuye con ningún momento (esto no es exclusivo de $\alpha$ constante, vale para cualquier estado de movimiento del rígido).

Por otro lado, la articulación horizontal (y el rígido en última instancia) está sometida a un par motor de manera de mantener la componente vertical de la velocidad angular al valor constante 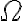$\Omega$ . Si uno resuelve un caso general del rígido en movimiento ( $\alpha$ variable en el tiempo), se encuentra con que ese par motor es proporcional a 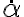$\dot \alpha$ , por lo que en las configuraciones donde $\alpha$ es constante, ese par es nulo.

Pero si vos partís de estudiar una configuración donde $\alpha$ es constante, al derivar el momento angular (visto desde $O$ ) te encontrás con que esa derivada no tiene componente vertical, por lo que es trivial (en el sentido matemático!) que no hay momento vertical aplicado (no sé como llegás al posible $\alpha$ ). Tenés entonces que usar de alguna forma que la articulación no ejerce momento en la dirección del eje (hay sí momento del peso en esa dirección) y que la derivada del momento angular apunta según esa misma dirección también.

Espero haber entendido bien tu duda,

saludos,

Ariel.

Re: Examen diciembre 2015, ejercicio 3

de Leandro Jair Machado Da Silva - sábado, 15 de agosto de 2020, 12:33

Ariel, muchas gracias por la respuesta!

La letra dice "En el punto O existe una articulación cilíndrica lisa, que obliga a la barra OC a moverse en un plano vertical que gira con velocidad angular constante Ω, en el sentido que muestra la figura". No entiendo cómo a partir de eso se entiende que la articulación es cilíndrica lisa de eje horizontal (si no mal recuerdo, ya me ha pasado esto de dudar según qué eje es lisa alguna articulación cilíndrica). Yo había entendido que, como la velocidad angular que impone tal articulación es según un eje vertical, la misma sería lisa de eje vertical también. Por lo que me comentas veo que no, pero no termino de entender cómo darme cuenta de eso a partir de la letra.

A modo de ejercicio extra, hice el planteo escribiendo 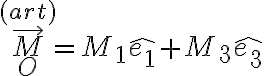$\vec{M}_O^{(art)}=M_1\hat{e_1}+M_3\hat{e_3}$ (con los versores de la solución) y llego a que 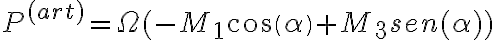$P^{(art)}=\Omega(-M_1cos(\alpha)+M_3sen(\alpha))$ por lo que el par motor del que hablas es 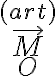$\vec{M}_O^{(art)}$ , verdad? (pregunto para ver si entendí bien el concepto de par motor) ya que, si 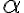$\alpha$ no fuera constante, aportaría energía al sistema. Pero como lo es, la energía se conserva (entonces, se podría encarar el ejercicio por este lado, no?) Gracias!

Re: Examen diciembre 2015, ejercicio 3

de Ariel Fernández - domingo, 16 de agosto de 2020, 03:38

Hola Leandro,

Si pensamos en el problema general (suponiendo $\alpha$ variable en el tiempo) de una barra (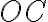 $OC$ ) que se mueve en el plano especifiicado, necesitás algún mecanismo de sujeción que permita el giro libre en ese plano; una articulación cilíndrica lisa, cuyo eje sea perpendicular al plano vertical indicado, es el mecanismo adecuado (y por ser perpendicular a un plano vertical, debe ser horizontal).

Ahora, esa articulación no ejerce momento según su eje pero sí puede hacerlo en el plano perpendicular y vamos a considerar en ese plano (que es en definitiva el que contiene a la barra 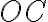$OC$ ) dos direcciones: la vertical, según la cual hay una velocidad angular impuesta 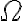$\Omega$ y una dirección más perpendicular tanto a la vertical como a la articulación en sí (usemos el versor 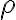$\rho$ de cilíndricas). El momento ejercido por la articulación lo escribo como:

$\vec M_O^{(art)}=M_k\hat k + M_\rho \hat e_\rho$

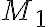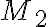y ahora voy a considerar el movimiento general del rígido (no puedo darte la idea del par motor con las condiciones mismas del ejercicio porque el momento de la articulación en sí da cero! Fijate que los $M_1$ y $M_3$ que nombrás son nulos y $M_2$ ya lo era por ser art. lisa):

$\vec \omega=-\dot \alpha \hat e_2+\Omega \hat k$ ,

donde incorporé la variación temporal de $\alpha$ a la velocidad angular. Si ahora hacemos el cálculo de la potencia como bien hiciste vos, nos queda:

$\mathcal{P}^{(art)}=\vec M_O^{(art)}\cdot\vec \omega=M_k\Omega$ .

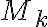Cuando está presente ( $\alpha$ variable), $M_k$ es el responsable de aportar energía al sistema y por eso le llamamos par motor. En cambio, cuando está presente, 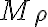$M_\rho$ no aporta energía pero evita que la barra se salga del plano (es lo que llamaríamos par reactivo nomás). Sin hacer el cálculo (podés intentarlo, claro!) te digo que cualquiera de los dos pares van con 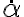$\dot \alpha$ , por lo que desaparecen para el caso particular del planteo del ejercicio.

Saludos,

Ariel.