Buenas haciendo este ejercicio me surgieron algunas dudas.
Letra:
Sea L2 = {w#w' / w ∈ L((0|1)*) y w' es su complemento bit a bit}
Parte b: Construya una gramática G2 / L(G2) = L2
La gramática que hice fue:
S -> X#
X -> 0UX | 1CX
U0 -> 0U
U1 -> 1U
C0 -> 0C
C1 -> 1C
U# -> #1
C# -> #0
X# -> #
La duda que tengo con esto es que en principio no logre romper mi gramática, si pueden lograrlo les agradezco un ejemplo.
Luego lo que me genera duda es si es correcto tener la producción X# -> # ya que en la solución usa algunas variables auxiliares para darle contexto al final cuando ya no se vaya a generar mas nada.
Parte c:
El autómata que hice fue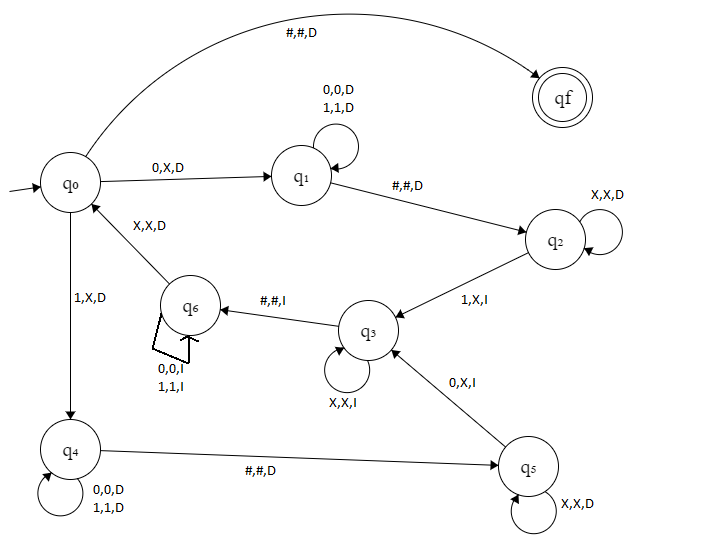
Quiero saber si la transición de q0 a qf es correcta o tengo que llegar a un blank como muestra la solución? A mi entender si leo #,#,D en q0 entonces ya procese todo el lado izquierdo y la tira era valida pero tal vez se me esta escapando algún caso o simplemente es obligación dejar el autómata en un blank y yo no lo recuerdo así.
En la solución usa marcas Y cuando pasa al lado derecho del #, son realmente necesarias por algo en especial o con el par de estados q3 y q6 que hice yo es lo mismo?
Gracias!
[2020] [Febrero] [Ejercicio 2] [Parte b y c]
Número de respuestas: 4[2020] [Febrero] [Ejercicio 2] [Parte b y c]
hola:
antes que nada, vuelvo a aclarar que las soluciones en teoría no son únicas... y que algo esté en las soluciones no quiere decir ni que sea la mejor forma, ni la más fácil ni la más sencilla de resolver un problema. dicho esto:
1- La duda que tengo con esto es que en principio no logre romper mi gramática, si pueden lograrlo les agradezco un ejemplo.
esto lo dejo para algun compañero del foro que tenga ganas de inspirarse ;-)
2- es correcto tener la producción X# -> # ya que en la solución usa algunas variables auxiliares para darle contexto al final cuando ya no se vaya a generar mas nada.
sí, es correcto. lo que tenés que asegurarte es que _toda_ derivación que termine en una tira de símbolos (sin variables) pertenezca al lenguaje y que toda tira del lenguaje sea derivable. mientras se cumpla lo anterior, si quedan derivaciones colgadas (con variables pero sin reglas a aplicar) no importa.
esto es: el cómo hacerlo queda a criterio (y elegancia) de quien redacta la solución.
3- A mi entender si leo #,#,D en q0 entonces ya procese todo el lado izquierdo...
el autómata no sabe si procesó todo el lado izquierdo o derecho. por ejemplo, ¿vos aceptás las siguientes tiras? porque no deberías.
- ###
- 10#010001110
- #lasnorequierenleertodalaentradasolollegaraunestadofinal (sería el codigo ascii en binario)
saludos,
d.-
[2020] [Febrero] [Ejercicio 2] [Parte b y c]
Diego. Gracias por tu respuesta. Respecto al punto 3 logre entender lo que dices pero me surgió una duda conceptual.
En el caso de la tira ### mi autómata con el primer # se va a qf y luego queda trancado en ese estado o se va a un estado pozo? Digo esto porque entendía que toda transición no definida iba a parar a un estado pozo.
Gracias
[2020] [Febrero] [Ejercicio 2] [Parte b y c]
hola:
en una máquina de turing, cuando se llega a un estado de aceptación, el autómata se detiene y acepta la tira. a diferencia de los otros modelos de autómatas, estas máquinas no requieren consumir toda la tira para su aceptación, con lo que la idea de estado pozo ("termino de procesar la tira") deja de tener sentido.
en tu caso, luego de leer el primer numeral la máquina llega a qF, se detiene y acepta la entrada sin mirar si hay o no más símbolos a su derecha: cualquier tira que comience con un numeral será aceptada por ese autómata.
saludos,
d.-
