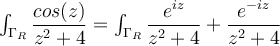Ejercicio de la clase de consulta de ayer

Ejercicio de la clase de consulta de ayer

de Agustin Tornaria Rodriguez -
Número de respuestas: 4
Hola! Ayer no pude asistir a la clase de consulta, pero ví el post que hizo Joaquin sobre el ejercicio del examen de julio de 2018 de la integral impropia.

Mi duda es porque no se puede aplicar el lema de deformación de caminos de una para luego aplicar el teorema de los residuos. Entiendo porque podés podés sumarle isin(x) pero no porque es necesario.

El hecho de sumar isin(x) hace que la integral no cambie por ser función impar, sin embargo el residuo te queda distinto, eso o estoy calculando algo mal.

Saludos y gracias!
En respuesta a Agustin Tornaria Rodriguez

Re: Ejercicio de la clase de consulta de ayer

de Joaquin Lejtreger -
Buenas,
Pongo el lema de Jordan acá para que lo veas junto a la respuesta.
m
Utilizando la definición del coseno complejo tenemos que

\int_{\Gamma_R} \dfrac{cos(z)}{z^2 + 4} = \int_{\Gamma_R} \dfrac{e^{iz}}{z^2 + 4} + \dfrac{e^{-iz}}{z^2 + 4}

En la segunda parte no podés aplicar el lema de Jordan porque el exponente no es positivo. Espero que esto haya contestado tu duda.

Saludos,
Joaquín
En respuesta a Joaquin Lejtreger

Re: Ejercicio de la clase de consulta de ayer

de Agustin Tornaria Rodriguez -

Buenas,

Entiendo lo que me decís del lema de Jordan que no lo podés aplicar ya que no cumple las hipótesis.

Pero sigo sin entender porque no podés usar este otro lema de deformación de caminos:

Lema de deformación de caminos

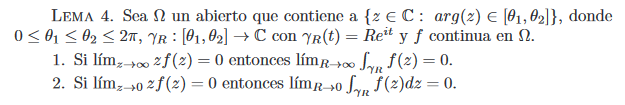
En las condiciones del ejercicio el limite de zf(z) = 0, tu curva es un semicircunferencia con lo que es de la forma pedida y f es continua.

Seguramente le estoy errando en alguna hipótesis pero no me logro dar cuenta.

Saludos.

En respuesta a Agustin Tornaria Rodriguez

Re: Ejercicio de la clase de consulta de ayer

de Joaquin Lejtreger -

El problema es que f(z) no tiende a 0 cuando z tiende a infinito. Si bien el coseno en la recta real está acotado, en el plano complejo no. De hecho esta función crece exponencialmente en las direcciones del eje imaginario. Por eso no se puede usar el de deformación de curvas.

Espero que esto ahora sí conteste tu duda.

Saludos,

Joaquín