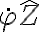Buenas, en este ejercicio el momento angular del rigido me quedo en función de la derivada de la velocidad angular del rígido y segun la dirección vertical, no se si estoy haciendo algo mal o tengo que suponer que la misma es constante.
Hola Pablo,
el momento angular del aro debería quedarte en términos de su velocidad angular: 
que tal como decís es vertical (quizás estés confundiendo el ángulo con la velocidad angular si mal no entiendo tu error, cualquier cosa preguntá de nuevo).
Saludos,
Ariel.
Claro, me quedo en función de 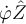, entonces como deduzco que la variación de ese momento angular es 0? osea que ese momento angular es constante.
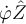, entonces como deduzco que la variación de ese momento angular es 0? osea que ese momento angular es constante.Lo que se me ocurio a mi tratando de deducir el resultado fue decir que como la articulación en B es cilíndrica lisa y el aro gira libremente entonces la aceleración angular del aro va a ser cero, Porque no hay una fuerza externa que acelere al aro ni tampoco una fuerza que se resista al giro para frenarlo. Pero no se si esta bien.
Gracias.
Hola Pablo,
tenés una fuerza reactiva ejercida por la partícula sobre el aro que va a afectar la velocidad angular del mismo, lo mejor en este caso es observar qué cantidades del sistema aro+partícula se conservan en el movimiento (fijate que esa interacción es interna al sistema y de potencia neta nula [es decir, el par acción-reacción no trabaja]).
Saludos,
Ariel.