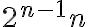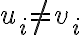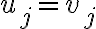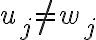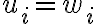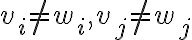Ejercicio 12 - Práctico 9

Ejercicio 12 - Práctico 9

de Ignacio Javier Acosta Rodriguez -
Número de respuestas: 3

Buenas tardes,

Tengo una duda respecto a la realización del ejercicio.

En la parte b, llegué a la conclusión de que los 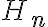H_{n} tenían 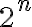2^{n} vértices que se corresponden los las distintas combinaciones de 0 y 1 que las n-uplas pueden tener.

Sin embargo no estoy seguro con la segunda parte, al hallar las aristas razoné que para que 2 grafos fueran adyacentes y existiera una arista entre los mismos, estos deben tener una sola entrada distinta. 

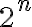Por ende creí que dado un vértice particular el mismo tiene n vértices adyacentes (son n entradas y puedo tener una distinta \binom{n}{1}), ese número que se relaciona con los adyacentes de un solo vértice lo multipliqué por 2^{n} que son la cantidad de vértices.

Sin embargo, no estoy contando aristas de más? (porque algunas son compartidas entre vértices).

Me podrían dar una idea de como demostrar que 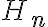H_{n} no tiene 3-ciclos?.

Muchas gracias.
En respuesta a Ignacio Javier Acosta Rodriguez

Re: Ejercicio 12 - Práctico 9

de Benjamin Montenegro Muniz -

Hola, mi razonamiento para las aristas fue como el tuyo lo unico que al multiplicar por 2^{n}n estás contando todas las aristas 2 veces,la arista a-b y la b-a son la misma, entonces hay que dividir por 2, quedaria 2^{n-1}n .

Para los 3-ciclos hice lo siguiente: si tenemos un ciclo de 3 con los puntos u=(u0,u1,...,ui,...uj ,...un) v=(v0,v1,...,vi,...vj ,...vn) y w=(w0,w1,...,wi,...wj ,...wn), donde u-v-w-u va a ser el ciclo, u-v entonces  u_{i}\neq v_{i} y  u_{j}= v_{j} porque solo se pueden diferenciar en una componente, ademas como u-w  u_{j} \neq w_{j} y  u_{i} = w_{i} y finalmente llegamos a que  v_{i} \neq w_{i},v_{j} \neq w_{j} por lo tanto v y w no están conectados y no se puede formar el ciclo de 3.

Yo esperaria la confirmación de un docente para ver si el razonamiento es correcto.


Saludos
En respuesta a Benjamin Montenegro Muniz

Re: Ejercicio 12 - Práctico 9

de Claudio Qureshi -

Hola.

En el conteo de Ignacio Acosta faltó solo observar que cada arista está contada dos vértices, la solución a la parte b de Benjamin es correcta.

La solución de Benjamin a la parte de probar que no hay 3-ciclos solo tiene un detalle. Faltó mencionar quienes son i y j. Por contexto concluyo que i es el lugar donde difieren u y v, mientras que j es el lugar donde difieren v y w. Además es importante observar que i es distinto de j caso contrario u sería igual a w contradiciendo la definición de ciclo. Ahora si, teniendo en cuenta lo anterior está correcto el remate: u y w no pueden ser adyacentes porque difieren en dos lugares (el lugar i y el lugar j). 

Esa de hecho es una estrategia general para probar que cierto grafo no tiene n-ciclos: considerarte caminos simples de longitud n-1 (o sea, que involucren n vértices) y probar que los vértices iniciales y finales no pueden ser iguales.

Usando esto de hecho se puede probar que Hn no tiene n-ciclos si n es impar (inténtelo!)