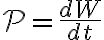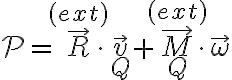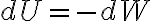Estimados Leandro y Juan,
para resolver la parte c) del ejercicio les recomiendo que consideren la definición de potencia:
de donde pueden hallar el diferencial de trabajo  .Ppor otro lado, la potencia de un sistema de fuerzas sobre un rígido es (ec. (8.6) Apuntes 2010)
.Ppor otro lado, la potencia de un sistema de fuerzas sobre un rígido es (ec. (8.6) Apuntes 2010)
(siendo 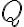 un punto arbitrario del rígido: eligiendo un punto
un punto arbitrario del rígido: eligiendo un punto 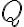 adecuado pueden usar lo hallado anteriormente).
adecuado pueden usar lo hallado anteriormente).
Directamente de la forma del  que van a encontrar es fácil ver que se trata de un sistema conservativo, por lo que se puede conectar este diferencial con el de la energía potencial asociada:
que van a encontrar es fácil ver que se trata de un sistema conservativo, por lo que se puede conectar este diferencial con el de la energía potencial asociada:
y a partir de allí, observando que 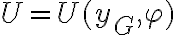 , pueden identficar las derivadas parciales e integrarlas para hallar la función energía potencial.
, pueden identficar las derivadas parciales e integrarlas para hallar la función energía potencial.
Saludos y suerte con el resto de las cuentas,
Ariel.