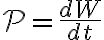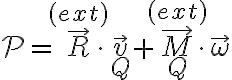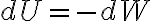Tengo un problema para llegar al momento, llego a (m(a²)(φ²)″)/3, no entiendo como llegar a ksen(φ)cos(φ)
Buenas!
Tenés que revisar como estás calculando ese momento:
Primero que nada tenés que ver el momento en cada punto de la barra e integrar.
Para empezar vas a tener el coseno que surge del producto vectorial entre la posición de cada punto y la fuerza (es el seno del ángulo entre esa posición y la fuerza, que geométricamente podés ver que es el coseno del phi).
Por otro lado, si te parás en el centro de gravedad de la barra, la altura del extremo derecho por ejemplo, sería a*sin(phi), y así para todos los puntos.
Espero haber sido claro, es medio dificil de explicar por acá pero cualquier duda preguntá de nuevo!
Suerte.
Gracias. Lo hice por donde decís y no se donde falle, pero llegue a 2a³/3, en ves de la solución. Tal vez con eso sepas donde me equivoque.
Sin ver tu solución es difícil saber dónde te equivocaste. Pero como dice Tomás,si no te aparece el coseno de φ estás haciendo mal el producto vectorial involucrado en el cálculo del momento.
Si el resultado al que te referís es a la integral que te aparece en el cálculo, te faltó multiplicar por la densidad de masa que es m/2a.
Hola, tengo una duda en la parte c, como calculo el trabajo infinitesimal?
Tengo la misma duda, no veo cómo usar los resultados de la parte a.
Estimados Leandro y Juan,
para resolver la parte c) del ejercicio les recomiendo que consideren la definición de potencia:
de donde pueden hallar el diferencial de trabajo 
.Ppor otro lado, la potencia de un sistema de fuerzas sobre un rígido es (ec. (8.6) Apuntes 2010)
(siendo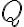 
un punto arbitrario del rígido: eligiendo un punto 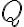adecuado pueden usar lo hallado anteriormente).
Directamente de la forma del que van a encontrar es fácil ver que se trata de un sistema conservativo, por lo que se puede conectar este diferencial con el de la energía potencial asociada:
y a partir de allí, observando que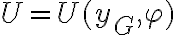 
, pueden identficar las derivadas parciales e integrarlas para hallar la función energía potencial.
Saludos y suerte con el resto de las cuentas,
Ariel.