No hay mucho más para seguir. Solo justificar que tras las rotaciones la altura del subárbol vuelve a ser la misma que antes de la inserción. Si eso ya está claro no hace falta leer el resto.
Supongamos que  es el nodo más profundo que queda desequilibrado tras una inserción. Por simplicidad, con un abuso de lenguaje vamos a darle el mismo nombre al nodo y al subárbol que lo tiene como raíz. A los hijos izquierdo y derecho de
es el nodo más profundo que queda desequilibrado tras una inserción. Por simplicidad, con un abuso de lenguaje vamos a darle el mismo nombre al nodo y al subárbol que lo tiene como raíz. A los hijos izquierdo y derecho de  les llamamos
les llamamos 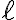 y
y  respectivamente. Sin pérdida de generalidad supongamos que la inserción se hizo en el subárbol izquierdo de
respectivamente. Sin pérdida de generalidad supongamos que la inserción se hizo en el subárbol izquierdo de  . Como se va a producir un desequilibrio sabemos que antes de la inserción la altura de
. Como se va a producir un desequilibrio sabemos que antes de la inserción la altura de 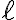 es mayor (uno más) que la de
es mayor (uno más) que la de  . Entonces si la altura de
. Entonces si la altura de  es
es  la de
la de 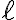 es
es  y la de
y la de  es
es  .
.
Como 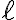 no es vacío tiene hijos, que sí pueden ser vacíos, y les llamamos
no es vacío tiene hijos, que sí pueden ser vacíos, y les llamamos 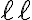 y
y 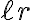 . La altura de ambos tiene que ser la misma,
. La altura de ambos tiene que ser la misma,  . Si no fuera así, como la inserción hace crecer la altura de
. Si no fuera así, como la inserción hace crecer la altura de 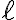 tiene que hacer crecer la altura del más alto de sus subárboles y como consecuencia
tiene que hacer crecer la altura del más alto de sus subárboles y como consecuencia 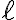 quedaría desequilibrado, lo que contradice la hipótesis original de que
quedaría desequilibrado, lo que contradice la hipótesis original de que  es el más profundo de los nodos que quedan desequilibrados.
es el más profundo de los nodos que quedan desequilibrados.
Ahora hay que distinguir dos casos: la inserción se hace en 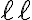 o en
o en 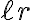 . La altura de ese subárbol va a pasar a ser
. La altura de ese subárbol va a pasar a ser  y como consecuencia la de
y como consecuencia la de 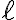 pasa a ser
pasa a ser  y la de
y la de  pasa a ser
pasa a ser 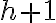 y además queda desequilibrado. La altura de algunos ancestros de
y además queda desequilibrado. La altura de algunos ancestros de  pudo aumentar y también quedar desequilibrados.
pudo aumentar y también quedar desequilibrados.
En este punto habría que hacer uno mismo un diagrama y luego verificar si coincide con esto.
- La inserción se hizo en
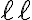 . Tras la rotación la raíz del árbol pasa a ser
. Tras la rotación la raíz del árbol pasa a ser 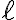 (en lugar de
(en lugar de  ). Su subárbol izquierdo es
). Su subárbol izquierdo es 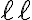 de altura
de altura  . Su subárbol derecho es
. Su subárbol derecho es  que también va a tener altura
que también va a tener altura  porque sus dos subárboles,
porque sus dos subárboles, 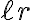 y
y  tienen altura
tienen altura  . Por lo tanto
. Por lo tanto 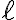 , la nueva raíz del árbol, tiene altura
, la nueva raíz del árbol, tiene altura  . Y la altura de los ancestros, si habían cambiado, también vuelven a ser la que tenían antes.
. Y la altura de los ancestros, si habían cambiado, también vuelven a ser la que tenían antes. - La inserción se hizo en
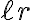 . A los hijos de este nodo después de la inserción vamos a llamarlos
. A los hijos de este nodo después de la inserción vamos a llamarlos 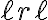 y
y 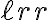 . Veamos que la altura de uno de ellos es
. Veamos que la altura de uno de ellos es  y la del otro es también
y la del otro es también  o
o  . Si
. Si 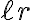 era vacío, lo que implica que
era vacío, lo que implica que  , sus dos subárboles tras la inserción van a ser vacíos, de altura
, sus dos subárboles tras la inserción van a ser vacíos, de altura  . Si
. Si 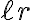 no era vacío sus dos subárboles antes de la inserción tenían altura
no era vacío sus dos subárboles antes de la inserción tenían altura  (tienen que ser iguales por la misma razón que tenían que ser iguales los subárboles de
(tienen que ser iguales por la misma razón que tenían que ser iguales los subárboles de 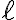 ). Como consecuencia uno para a tener altura
). Como consecuencia uno para a tener altura  y el otro queda en
y el otro queda en  . Lo importante es que la altura de ambos no es mayor a
. Lo importante es que la altura de ambos no es mayor a  . Como consecuencia de las rotaciones la nueva raíz es
. Como consecuencia de las rotaciones la nueva raíz es 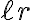 . Su subárbol izquierdo es
. Su subárbol izquierdo es 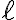 que tiene altura
que tiene altura  porque sus subárboles son
porque sus subárboles son 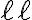 de altura
de altura  y
y 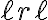 de altura
de altura  o
o  . Su subárbol derecho es
. Su subárbol derecho es  que también tiene altura
que también tiene altura  porque sus subárboles son
porque sus subárboles son 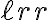 de altura
de altura  o
o  , y
, y  de altura
de altura  . Por lo tanto, también en este caso el subárbol que antes tenía a
. Por lo tanto, también en este caso el subárbol que antes tenía a  en la raíz vuelve a tener altura
en la raíz vuelve a tener altura  .
.
