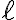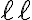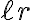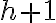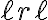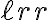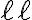Prog2: Insercion y borrado de un AVL

Buenas, el las diapositivas aparece que el orden de insercion usando lazy deletion no se puede hacer en O(logn) y no me queda claro porque. Ademas porque luego de insertar en un AVL , en caso de encontrar un nodo a rotar, es necesario solo rotar ese nodo ? No se debe seguir la recursion para seguir actualizand las alturas de todo el camino/ rotar otro eventuales nodos? (Ponen que no en las diapositivas, pero no termino de entender porque)

Ademas , que otros mecanismos de borrado se pueden implementar en un AVL si es necesario mantener O(logn) en las inserciones?

Re: Insercion y borrado de un AVL

de Fernando Fernandez - sábado, 30 de mayo de 2020, 15:19

Vamos de a una por vez. ¿Por qué alcanza con equilibrar un subárbol (o nodo) tras una inserción? De todas formas, no es uno cualquiera en el que hay que hacer las rotaciones, sino en el más profundo de los que quedaron desequilibrados.

La versión corta es que al reequilibrar un subárbol que había quedado desequilibrado su altura vuelve a ser la que tenía antes.

Para desarrollar lo anterior tal vez convenga preguntarse por qué tras una inserción habría más de un subárbol desequilibrado (por ejemplo, ¿al remover puede quedar más de uno desequilibrado?).

Para que como consecuencia de una inserción en un árbol con propiedad de estructura AVL un subárbol $u$ quede desequilibrado tiene que ocurrir que la inserción se haga en su subárbol estrictamente más alto y además que la altura de ese subárbol aumente. Como consecuencia la altura de $u$ aumenta. Y como esta es una de las condiciones necesarias para que su padre, llamémosle $p$ , quede desequilibrado es posible que $p$ y recursivamente una secuencia de ancestros también queden desequilibrados (de manera transitoria).

Si al hacer las rotaciones el subárbol $u$ vuelve a tener la misma altura que tenía antes en ninguno de sus ancestros queda modificada la altura que tenían sus subárboles antes de la inserción por lo que no cambia su factor de balance y siguen equilibrados.

Entonces si estas rotaciones se hacen en el más profundo de los subárboles que habían quedado desequilibrados todo el árbol recupera la propiedad de estructura AVL.

Quedo por ahí un 'si': que al hacer las rotaciones la altura del subárbol vuelve a ser la anterior. Aceptando provisoriamente esto, ¿quedaría claro por qué alcanza con reequilibrar un subárbol?

Re: Insercion y borrado de un AVL

de Rafael Agustin Castelli Ottati - domingo, 31 de mayo de 2020, 12:03

Si, te sigo en el razonamiento.

Re: Insercion y borrado de un AVL

de Fernando Fernandez - martes, 2 de junio de 2020, 11:11

No hay mucho más para seguir. Solo justificar que tras las rotaciones la altura del subárbol vuelve a ser la misma que antes de la inserción. Si eso ya está claro no hace falta leer el resto.

Supongamos que $u$ es el nodo más profundo que queda desequilibrado tras una inserción. Por simplicidad, con un abuso de lenguaje vamos a darle el mismo nombre al nodo y al subárbol que lo tiene como raíz. A los hijos izquierdo y derecho de $u$ les llamamos $\ell$ y $r$ respectivamente. Sin pérdida de generalidad supongamos que la inserción se hizo en el subárbol izquierdo de $u$ . Como se va a producir un desequilibrio sabemos que antes de la inserción la altura de $\ell$ es mayor (uno más) que la de $r$ . Entonces si la altura de $u$ es $h$ la de $\ell$ es $h-1$ y la de $r$ es $h-2$ .

Como $\ell$ no es vacío tiene hijos, que sí pueden ser vacíos, y les llamamos $\ell \ell$ y $\ell r$ . La altura de ambos tiene que ser la misma, $h-2$ . Si no fuera así, como la inserción hace crecer la altura de $\ell$ tiene que hacer crecer la altura del más alto de sus subárboles y como consecuencia $\ell$ quedaría desequilibrado, lo que contradice la hipótesis original de que $u$ es el más profundo de los nodos que quedan desequilibrados.

Ahora hay que distinguir dos casos: la inserción se hace en $\ell \ell$ o en $\ell r$ . La altura de ese subárbol va a pasar a ser $h-1$ y como consecuencia la de $\ell$ pasa a ser $h$ y la de $u$ pasa a ser $h+1$ y además queda desequilibrado. La altura de algunos ancestros de $u$ pudo aumentar y también quedar desequilibrados.

En este punto habría que hacer uno mismo un diagrama y luego verificar si coincide con esto.

La inserción se hizo en $\ell \ell$ . Tras la rotación la raíz del árbol pasa a ser $\ell$ (en lugar de $u$ ). Su subárbol izquierdo es $\ell \ell$ de altura $h-1$ . Su subárbol derecho es $u$ que también va a tener altura $h-1$ porque sus dos subárboles, $\ell r$ y $r$ tienen altura $h-2$ . Por lo tanto $\ell$ , la nueva raíz del árbol, tiene altura $h$ . Y la altura de los ancestros, si habían cambiado, también vuelven a ser la que tenían antes.
La inserción se hizo en $\ell r$ . A los hijos de este nodo después de la inserción vamos a llamarlos $\ell r \ell$ y $\ell r r$ . Veamos que la altura de uno de ellos es $h-2$ y la del otro es también $h-2$ o $h-3$ . Si $\ell r$ era vacío, lo que implica que $h-2 = 0$ , sus dos subárboles tras la inserción van a ser vacíos, de altura $h-2$ . Si $\ell r$ no era vacío sus dos subárboles antes de la inserción tenían altura $h-3$ (tienen que ser iguales por la misma razón que tenían que ser iguales los subárboles de $\ell$ ). Como consecuencia uno para a tener altura $h-2$ y el otro queda en $h-3$ . Lo importante es que la altura de ambos no es mayor a $h-2$ . Como consecuencia de las rotaciones la nueva raíz es $\ell r$ . Su subárbol izquierdo es $\ell$ que tiene altura $h-1$ porque sus subárboles son $\ell \ell$ de altura $h-2$ y $\ell r \ell$ de altura $h-2$ o $h-3$ . Su subárbol derecho es $u$ que también tiene altura $h-1$ porque sus subárboles son $\ell r r$ de altura $h-2$ o $h-3$ , y $r$ de altura $h-2$ . Por lo tanto, también en este caso el subárbol que antes tenía a $u$ en la raíz vuelve a tener altura $h$ .

Entonces en ambos casos la altura del árbol vuelve a ser

$h$ como antes de la inserción. Si algún ancestro había quedado temporalmente desequilibrado vuelve a quedar bien equilibrado después de las rotaciones.