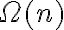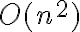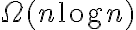Buenas, intenté resolver el ejercicio que proponían en las diapositivas sobre los órdenes de intersección/diferencia/unión para conjuntos representados por ABB y quisiera saber si lo que pensé está bien.
Creo que cualquiera de las operaciones se pueden hacer en O(n + m) donde n y m son la cardinalidad de ambos conjuntos, con el siguiente procedimiento:
Primero linealizo los arboles a una lista ordenada donde las inserciones al principio y al final sean de O(1). Linealizar ambos arboles es O(max{n, m}). Luego de eso, traduzco la lista a un árbol degenerado lo que es O(n), y ese es mi resultado.
La otra alternativa, que creo que es mejor porque no me devuelve un árbol degenerado en general sería:
Calculo las cardinalidades de ambos conjuntos, esto es O(max{n, m}).
Inserto los elementos de un árbol en un arreglo de tamaño n, y los del otro en uno de tamanio m. Esto con una recorrida inOrder es O(max{n, m}). Luego, paso el resultado de la operación a un arreglo de tamaño n + m, con tope (de la misma forma que hacía con las listas ordenadas). Esto me queda O(n + m).
Ahora traduzco el arreglo resultado a un ABB, creando un árbol vacío e insertando nodos. La inserción la hago insertando los puntos medios. O sea, si tengo un arreglo de tamaño n lo cubro primero insertando el elemento en n/2. Luego los elementos en n/4 y 3n/4 y así sucesivamente. Suponiendo que las claves de los elementos se distribuyen uniformemente, en promedio el árbol debería quedar “bastante balanceado”.
La otra solución que se me ocurrió es simplemente recorrer todos los nodos de un árbol, y preguntar si están en el otro árbol o no, y según eso insertar en un árbol nuevo. El problema es que creo que esto quedaría de O(nlog(m)) en promedio y O(n*m) en el peor caso.
Respecto a todo esto tengo las siguientes preguntas:
1) ¿Están bien ambas resoluciones al problema? ¿Hay alguna forma mejor de hacerlo?
2) Cuando pido/borro un arreglo el orden de ejecución es O(n) u O(1)?
3) Asumiendo que el segundo procedimiento está bien (el de los arreglos), realmente es más rápido este algoritmo que el que es O(n*log(m)) en promedio? La pregunta viene por lo siguiente. Si bien tengo algo de O(n + m), las constantes que quedan en la expresión deberían ser “bastante más grandes” que las constantes en el caso nlog(m), entonces tengo una cota k(n+m). Para nlog(m) tengo algo del estilo h nlog(m) donde k es “bastante más grande que h”. Entonces eligiendo m como el más grande de los números, puedo llegar a tener que incluso para m muy grandes k(n+m) > h*nlog(m). Entonces cual algoritmo sería “más rápido” en este caso, o preferible en tiempo de ejecución.