Hola.
Vamos a ver las de semánticas aquí: la de completitud, posteala en completitud. (Sólo para mantener el orden).
1) Cómo probaría que una fórmula NO es satisfactible?
Bueno, yo creo que analizaría las definiciones y probaría a través del contrarecíproco..
La negación (o mejor dicho el contrarecíproco) sería que:
Esto último nos da la pista de los que hay que probar:
Probando eso, estaríamos probando que no es satisfactible. Luego en el curso, vamos a ver una forma concreta de probar esto.
Dada la fórmula en general es posible hacer esto pero, posiblemente, convenga discutir los casos de sentencia y no sentencia.
2) Si dos formulas son equivalentes en una estructura M1, son equivalentes en una estructura M2 que cumpla con los tipos de similaridad? En el caso que sea correcto, es asi como se demuestra la propiedad que viene despues del teorema de sustitucion?
Cuidado con la formulación. Tu pregunta no es sobre la propiedad que viene después del teorema de sustitución. Esa propiedad dice:
O sea, si tenemos dos formulas equivalentes (en cualquier estructura), entonces si ponemos cada una de esas fórmulas en los mismos lugares de una misma tercer fórmula, el resultado son fórmulas equivalentes (en cualquier estructura). Y eso es independiente de la condición de "libertad con respecto a $".
Yo tomaría 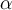 y
y 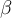 arbitrarios y equivalentes y trabajaría la tesis tomando una estructura arbitraria, haciendo una inducción sobre
arbitrarios y equivalentes y trabajaría la tesis tomando una estructura arbitraria, haciendo una inducción sobre 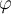 .
.
El teorema es diferente con respecto al de sustitución por las meta-cuantificaciones sobre las estructuras: En sustitución hay una sola, aquí hay dos.
Saludos
FDO.
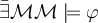
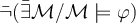
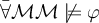
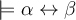
![\models \varphi[\alpha/\$] \leftrightarrow \varphi[\beta/\$] \models \varphi[\alpha/\$] \leftrightarrow \varphi[\beta/\$]](https://eva.fing.edu.uy/filter/tex/pix.php/938dc313bd3a86e0d59e2545cc5ba627.png)