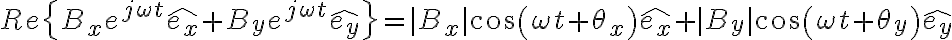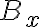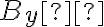Primer parcial 2017 Problema 1

Primer parcial 2017 Problema 1

de Jeremias Laporte Susenna -
Número de respuestas: 5

Buenas tardes,

Estaba realizando este problema y no me queda claro como realizar las partes 4a) y 4b). Se cuando tengo cada polzarizacion (Lo que se pide en la parte 4)), pero en la parte a) no se como hallar la orientación del eje mayor, razón entre sus ejes y sentido de giro. En la parte b) supongo que tengo que tener By = 0 pero no se como hacer para que sea vertical (se me ocurrio que Bx sea imaginario puro pero no estoy seguro de que este correcto).

Saludos,

Jeremias.

En respuesta a Jeremias Laporte Susenna

Re: Primer parcial 2017 Problema 1

de Juan Pablo Gonzalez Rivero -

Hola, 


4a. Mirando el sentido de giro del campo eléctrico (al aumentar el tiempo) de la onda que se aleja

del observador, se ve que el mismo es contrario al sentido de las agujas del reloj, por lo que

diremos que se tiene una polarización elı́ptica a izquierdas para los valores de k considerados.

En particular si 0.5 <= k < 1, el eje mayor está alineado al eje x de coordenadas y el menor al eje -1

y de coordenadas y la relació n entre eje mayor y menor es k . Cuando k >1 el eje mayor está alineado al eje y y el menor al eje x y la relació n entre eje mayor y eje menor es k. Si k=1 se trata de una polarizació n circular.

4b. En este caso la componente Ey=0, entonces By=0, lo que ocurre si k=0.


En respuesta a Juan Pablo Gonzalez Rivero

Re: Primer parcial 2017 Problema 1

de Mateo Trujillo Diaz -

Hola, no me doy cuenta en la parte 1a cómo hacés para darte cuenta que el campo gira en sentido antihorario.

Alcanza con ver que tanto Bx como By están multiplicados por e^(jwt)?

En respuesta a Mateo Trujillo Diaz

Re: Primer parcial 2017 Problema 1

de Juan Pablo Gonzalez Rivero -

Tenes que pensar que el campo físicamente es  Re\{B_x e^{j\omega t} \hat{e_x} +B_y e^{j\omega t} \hat{e_y} \} = |B_x|cos(\omega t+\theta_x) \hat{e_x}+ |B_y|cos(\omega t+\theta_y)\hat{e_y} .

Si ahora pensas en como se mueve el vector a medida que avanza t (dependiendo de las fases de   B_x y   B_y  y sus modulos) vas a tener un vector de campo total que se mueve en una dirección o en otra, formando una linea, elipse o circulo y en que sentido gira.