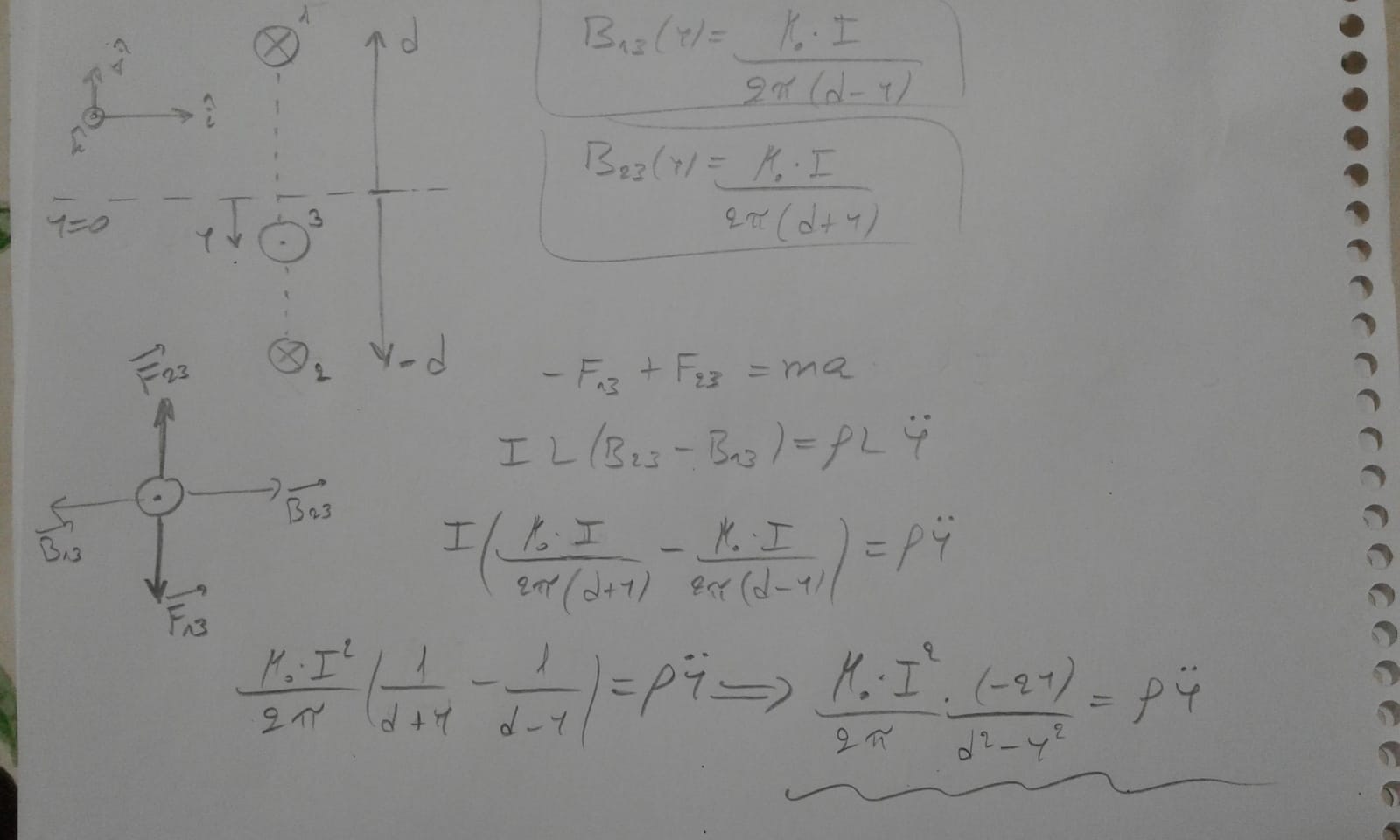Hola. Llegue a un punto en el que me tranque. Necesitaría una mano para ver como seguir. Ahí paso foto de un resumen de lo que hice.
Qué tal Juand Pedro?
Ya casi lo tenes! Lo único que te falta es considerar que y<<d (condición de pequeñas oscilaciones) para simplificar el denominador y luego recordar la ecuación del oscilador (lo más fácil puede ser recordar la frecuencia de oscilación de un sistema masa resorte).
Espero que esto te ayude!
Saludos,
Daniel Gau.
Hola, yo llegué a lo mismo que el compañero pero no se como usar que y<
(1/d+y)-(1/d-y)= (1/d)-(1/d)=0, y esto no tiene mucho sentido.
Probablemente no sea así la forma de usarlo, pero no se me ocurre como.
Tampoco me acuerdo mucho de oscilaciones, creo que para hallar la frecuencia angular estoy buscando algo así:
y''+(w^2)y+C=0.
Si me pudieran guiar sería de mucha ayuda.
Gracias, saludos.
Probablemente no sea así la forma de usarlo, pero no se me ocurre como.
Tampoco me acuerdo mucho de oscilaciones, creo que para hallar la frecuencia angular estoy buscando algo así:
y''+(w^2)y+C=0.
Si me pudieran guiar sería de mucha ayuda.
Gracias, saludos.
Qué tal María?
Lo que tenes que hacer ahora es la resta en esa expresión que escribiste, pero sin simplificar todavía. Eso te va a dar el resultado de la última ecuación de la imagen, donde ahora sí podes despreciar el término en y^2, pero conservando la dependencia en y.
'Tampoco me acuerdo mucho de oscilaciones, creo que para hallar la frecuencia angular estoy buscando algo así:
y''+(w^2)y+C=0.'
Esto que pensas está bien. Fijate que haciendo lo que te comenté arriba vas a llegar a una expresión de esta forma, donde lo único que tenes que hacer es identificar quien es w^2. Esa va a ser la frecuencia angular que buscas.
Espero que esto te pueda ayudar.
Saludos,
Daniel Gau.
Lo que tenes que hacer ahora es la resta en esa expresión que escribiste, pero sin simplificar todavía. Eso te va a dar el resultado de la última ecuación de la imagen, donde ahora sí podes despreciar el término en y^2, pero conservando la dependencia en y.
'Tampoco me acuerdo mucho de oscilaciones, creo que para hallar la frecuencia angular estoy buscando algo así:
y''+(w^2)y+C=0.'
Esto que pensas está bien. Fijate que haciendo lo que te comenté arriba vas a llegar a una expresión de esta forma, donde lo único que tenes que hacer es identificar quien es w^2. Esa va a ser la frecuencia angular que buscas.
Espero que esto te pueda ayudar.
Saludos,
Daniel Gau.