Necesitaría alguna idea de como resolver el ejercicio.
Gracias
Hola Nahuel,
tanto el punto 
como el punto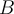 
tienen un movimiento circular: en el caso de uniforme y radio 
, en el caso de 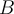no uniforme (lo vas a ver un poco más adelante) y de radio 
.
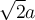Para determinar cómo se mueve 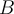, comenzá por definir un ángulo (
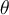) que forma 
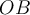con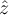 
; viendo luego la placa "desde arriba" (es decir, proyectada sobre el plano 
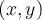) podés vincular 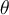con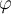 
.
SI derivás luego la relación hallada anteriormente, vas a poder vincular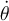 
con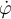 
que son los que determinan la velocidad de los puntos y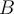 
respectivamente. Con eso tenés al final la relación entre velocidades que se pide.
Suerte y si al avanzar el problema te surge alguna duda, preguntá nomás.
Saludos,
Ariel.
Ariel, yo a esta parte la hice con coord. cartesianas, use que dφ/dt = va /a metiendolo al derivar la posicion de B. Mi pregunta es, lo que tu planteas es hacer coord. cilíndricas para A y para B verdad? Pero no se como ejecutar la idea de ''mirar desde arriba'' para relacionar φ y θ. Gracias
Hola Nicolás,
a lo que iba con ver de arriba la placa se explica mejor con un dibujo (le agregué al del ejercicio lo necesario para la explicación), es todo geometría y trigonometría pero es parte de la visualización en el espacio que la asignatura fomenta:
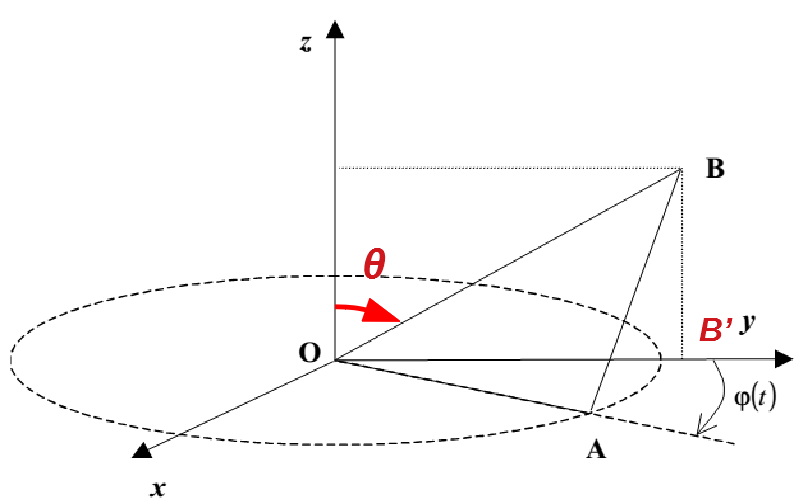
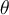: ángulo que forma OB con el eje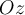 
B': proyección de B en el eje 
Si ves "de arriba" la placa, es decir, proyectás la misma en el plano 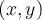, vas a encontrarte con el tríángulo OAB' que tiene:
-
-lado OA=
-lado OB' que podés escribir fácilmente en términos de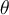
-
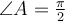: este punto es crucial, podés ver que es así considerando por ejemplo que el plano que pasa por A,B y B' es perpendicular a OA (AB es perpendicular a OA, BB' también por ser vertical), por lo que cualquier recta contenida en ese plano (AB' lo está) es perpendicular a OA
Con este último punto cubierto tenés entonces que el triángulo OAB' es rectángulo en A, con un poco de trigonometría hallás la relación entre 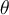y 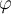y derivándola en el tiempo, la relación entre 
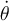y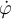 
, con lo que podés relacionar las velocidades de A y B.
Saludos y suerte,
Ariel.
Buenas, no estoy logrando entender el movimiento del sistema en total, mas que nada que pasa en el punto B porque de permanecer cte en la coordenada z el ángulo tita no variaría, ósea el punto B estaría bajando?
Estimado:
En efecto, a medida que
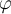aumenta, B baja (ni la altura de B ni 
son constantes). Pero B baja moviéndose en una circunferencia de centro O y radio OB constante en el plano Oyz. Observar que el triángulo OAB es isosceles y rectángulo en A. O sea que si a son sus catetos, OB que es la hipotenusa, valdrá siempre ![\sqrt[]{2}a](https://eva.fing.edu.uy/filter/tex/pix.php/94c4fe28ab960d3d12b1487b650e904b.png "\sqrt[]{2}a")
.
En efecto, a medida que
aumenta, B baja (ni la altura de B ni son constantes). Pero B baja moviéndose en una circunferencia de centro O y radio OB constante en el plano Oyz. Observar que el triángulo OAB es isosceles y rectángulo en A. O sea que si a son sus catetos, OB que es la hipotenusa, valdrá siempre . Saludos:
Ricardo.