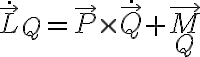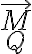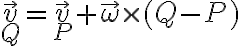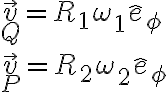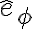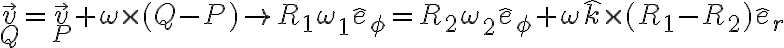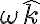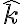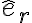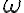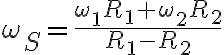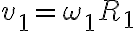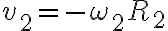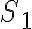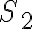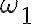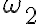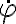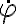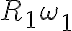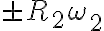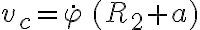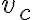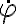Me acabo de dar cuenta de que me confundí y respondí sobre el ejercicio 5, no el 8, perdón, mala mía.
En este ejercicio la idea es usar distribución de velocidades: La velocidad de un punto Q de un rígido se puede escribir en términos de la de otro punto P también del rígido y de la velocidad angular del mismo:
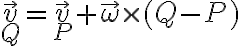
Para empezar con la parte a) podés usar que hay rodadura sin deslizar: Cuando hay rodadura sin deslizamiento, la velocidad en el punto de contacto es igual para ambos rígidos. Como el disco se está moviendo sin deslizar entre ambos aros, la velocidad en los puntos de contacto (Q y P) es igual a la velocidad que te da la letra de los discos (que giran a velocidad angular constante):
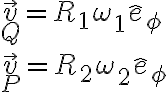
Siendo 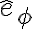 el versor tangencial de coordenadas polares planas. Luego podés usar distribución de velocidades entre P y Q:
el versor tangencial de coordenadas polares planas. Luego podés usar distribución de velocidades entre P y Q:
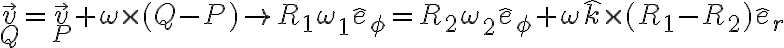
donde 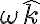 es la velocidad angular del disco, que si bien aún es desconocida, por ser el movimiento plano podemos suponer que su dirección es vertical (versor
es la velocidad angular del disco, que si bien aún es desconocida, por ser el movimiento plano podemos suponer que su dirección es vertical (versor 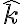 ). El versor
). El versor 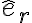 es el versor radial de coordenadas polares planas.
es el versor radial de coordenadas polares planas.
De esta última ecuación se puede despejar 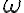 , y la dirección ya sabemos que es
, y la dirección ya sabemos que es 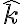 .
.