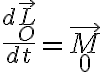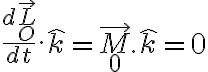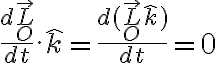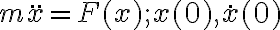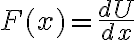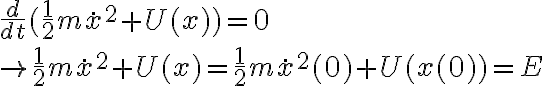Foro Práctico IV

La energía se conseva porque las fuerzas que actúan sobre la partícula son el peso, la fuerza del resorte (ambas conservativas) y la reacción normal a la superficie (de potencia nula). 

La conservación de la componente vertical del momento angular con respecto al punto O se puede probar usando la segunda cardinal. Como el punto O es fijo, se tiene que

$\frac{d \vec{L}_O}{dt} = \vec{M}_0$

Como el momento de las fuerzas externas en la dirección vertical es cero:

$\frac{d \vec{L}_O}{dt} . \hat{k} = \vec{M}_0 . \hat{k} = 0$

Además, el versor vertical es constante:

$\frac{d \vec{L}_O}{dt} . \hat{k} = \frac{ d ( \vec{L}_O \hat{k} ) }{dt} = 0$

Entonces, la componente vertical del momento angular con respecto al punto O es constante en el tiempo. 

Sobre la segunda parte de la pregunta: Por qué se necesitan dos leyes de conservación para describir el movimiento? 

En realidad, se necesitan dos ecuaciones diferenciales (y sus condiciones iniciales) para poder resolver el movimiento porque hay dos grados de libertad: La partícula está restringida a moverse en una superficie bidimensional. Si estuviera libre en el espacio, serían tres grados de libertad (tres ecuaciones dif. necesarias) y si estuviera restringida a moverse en una recta o en una curva cualquiera, tendría un grado de libertad y con una ecuación diferencial bastaría. 

Si el problema es conservativo (o si hay cantidades conservadas en general, ya sea la energía u otra cosa), una ley de conservación es una ecuación diferencial válida si se tienen las condiciones iniciales necesarias. Tratar de entender esto por primera vez en un ejercicio como el del parcial puede no ser lo mejor, así que vamos a verlo en un ejemplo más simple y transparente. Si tenemos una partícula que se mueve en una dimensión bajo la acción de una fuerza, su movimiento se puede describir con la ecuación de Newton y teniendo la posición y velocidad a tiempo inicial (cero por ejemplo):

$m \ddot{x} = F(x); x(0),\dot{x}(0)$

En el caso de que la fuerza sea conservativa, esta deriva de un potencial:

$F(x)=\frac{dU}{dx}$

Usando esto en la ecuación de movimiento y multiplicando ambos lados por 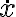$\dot{x}$ se puede preintegrar la ecuación (ver teórico):

$\frac{d}{dt} ( \frac{1}{2} m \dot{x}^2 + U(x) ) = 0 \\ \rightarrow \frac{1}{2} m \dot{x}^2 + U(x) = \frac{1}{2} m \dot{x}^2(0) + U(x(0)) = E$

Teniendo las condiciones iniciales de la posición y la velocidad se obtiene la energía E y entonces la ecuación anterior es una ecuación diferencial perfectamente válida para describir el movimiento de la partícula. Acá podemos decir que "necesitamos una ley de conservación" para describir la dinámica, en realidad es simplemente obtener la ecuación de movimiento.

En el problema del parcial, se podrían hallar las ecuaciones de movimiento por Newton en vez de usar conservación de la energía.Al preintegrarlas, se puede verificar que son equivalentes a las leyes de conservación (asimismo, derivando las leyes de conservación con respecto al tiempo, se obtienen ecuaciones equivalentes a las obtenidas por Newton).