Hola, para resolver este ejercicio (parte a) nos tomamos una superficie gaussiana esférica concéntrica con la que nos dan, y aplicamos Gauss restringiéndonos al eje z, la carga encerrada sería la que se considera en la solución para la esfera, más 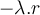 , donde
, donde 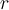 es el radio de la superficie gaussiana tomada. Mi pregunta es, ¿por qué está mal esto? ya que obtenemos un resultado parecido al de la solución, pero no es el mismo, obtenemos
es el radio de la superficie gaussiana tomada. Mi pregunta es, ¿por qué está mal esto? ya que obtenemos un resultado parecido al de la solución, pero no es el mismo, obtenemos ![\vec{E}(z)=[\frac{\rho}{3\epsilon_o}z - \frac{\lambda}{4\pi\epsilon_oz}]\hat{k} \vec{E}(z)=[\frac{\rho}{3\epsilon_o}z - \frac{\lambda}{4\pi\epsilon_oz}]\hat{k}](https://eva.fing.edu.uy/filter/tex/pix.php/56a4f20d7d6435e45b7bfa28e554d759.png) para
para 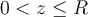
Primer parcial segundo semestre 2016 -Ejercicio 1
Número de respuestas: 2Re: Primer parcial segundo semestre 2016 -Ejercicio 1
Qué tal Leandro?
Este resultado no es correcto porque una superficie esférica solamente puede considerarse Gaussiana si la distribución de carga tiene una simetría esférica. Esto solo se cumple si se considera solamente la densidad de carga Ω de la esfera. En este caso el módulo del campo eléctrico es igual sobre toda la superficie y además el vector campo eléctrico y la normal saliente a la esfera son colineales haciendo que la integral sea fácil de calcular. Si ahora agregamos la barra con la densidad de carga lambda la simetría esférica se rompe haciendo que la superficie esférica ya no sea Gaussiana.
Lo que es importante notar es que el campo producido en el punto de interés solamente por la distribución de carga esférica sí puede calcularse con el razonamiento que hicimos inicialmente. Luego, para obtener el resultado buscado se debe sumar el campo producido por la barra que puede calcularse por integración directa, como lo hacen en la solución.
Saludos,
Daniel Gau.
Re: Primer parcial segundo semestre 2016 -Ejercicio 1
Genial! Muchas gracias!!