Buenas,
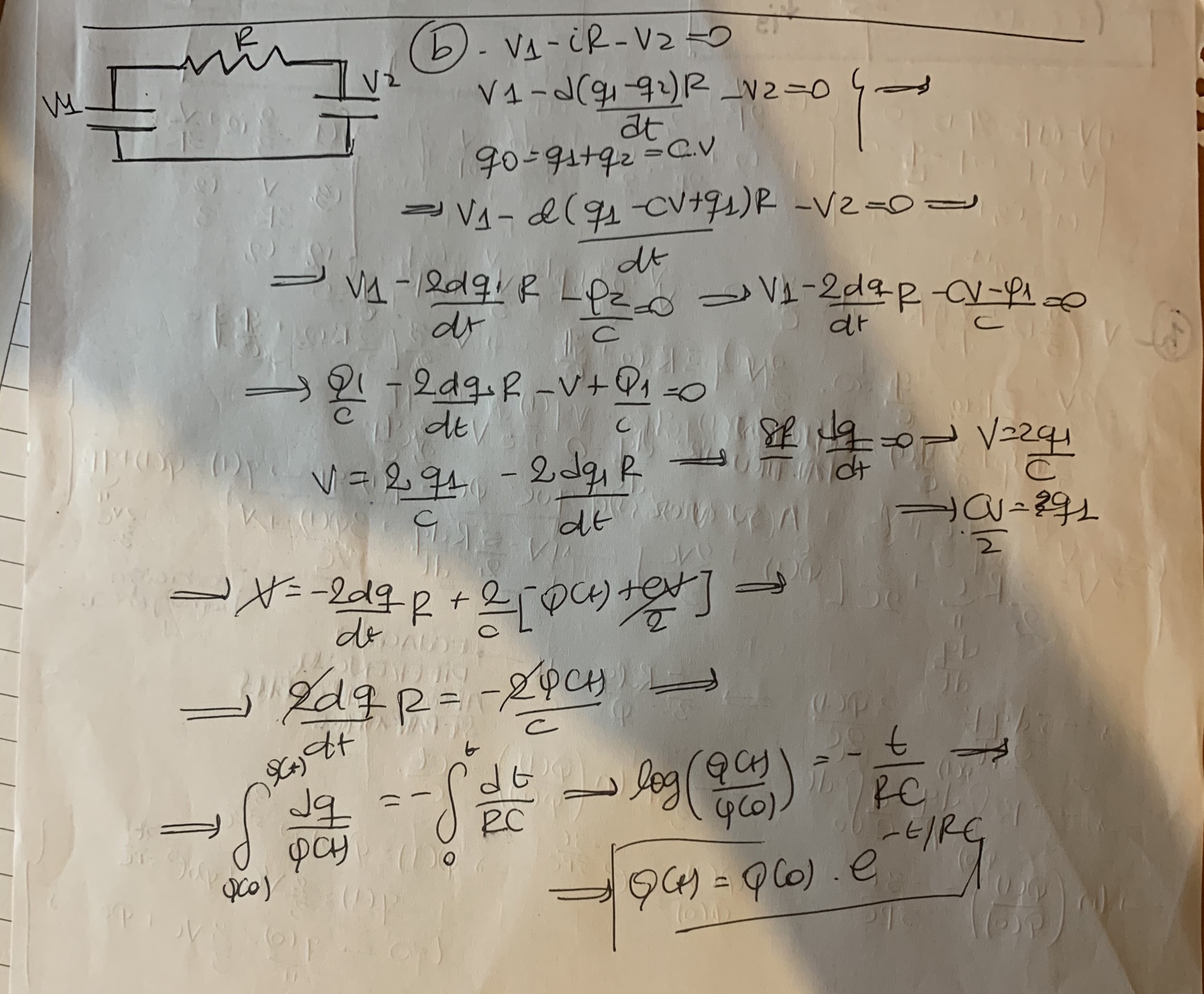
En la solución de este ejercicio, en la parte b dice que Q1(t)=Q0/2(1+e^(-2t/RC))
No entiendo de dónde sale el 2 de la exponencial, según lo que hice yo me queda e^(-t/RC).
Dejo una foto de mi procedimiento,
Gracias!
En respuesta a Juan Manuel Cabrera Barrera
Re: 1er parcial, 8/5/12 ejercicio 1)
Hola Juan Manuel,
la relación entre la intensidad y las cargas no es como la escribís.
Notá que la disminución de la carga en C1 es el aumento de la carga en C2.
Esto es, i = - dq1/dt = + dq2/dt
La relación entre las cargas sí es correcta, la suma de q1 y q2 en todo momento debe ser igual a la carga inicial Q=CV.
Saludos!
En respuesta a Florencia Benitez Martinez
Re: 1er parcial, 8/5/12 ejercicio 1)
Buenas, he hecho las cuentas para hallar el voltaje en C1, planteando Kirchhoff y resolviendo la ecuacion diferencial para la descarga de C1 y he llegado a que Q1(t)= Qoe^(-2t/RC); No entiendo como se llega a la solución subida.
Qo/2 no es la carga final que tienen ambos condensadores luego de un tiempo largo? No entiendo por qué aparece en la expresión de C1. Cualquier ayuda me viene bien.
Gracias
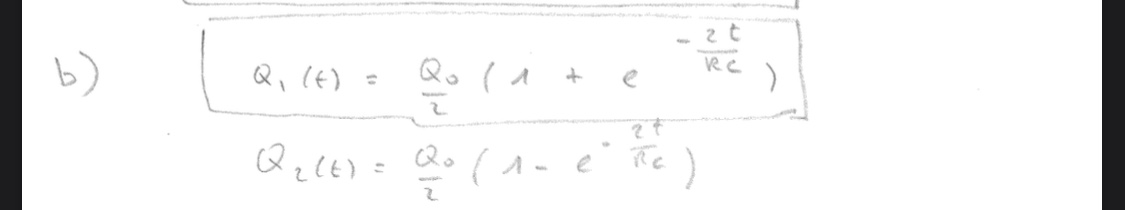
Te dejo esta otra discusión sobre el mismo ejercicio
https://eva.fing.edu.uy/mod/forum/discuss.php?d=160861
fijate que tu expresión para Q1 no cumple lo que decís (cuando t->infinito tu Q1 tiende a 0 no a Q0/2)
Una ecuación diferencial necesita de condiciones, en este caso una de las condiciones es : t->infinito, Q1 tiende a Q0/2 y t=0 Q=Q0, tu solución tiene que respetar eso.
Si no es claro subí lo que hiciste y lo miramos.
Saludos!