Buenos días.
Estimados,
Parte a)
Probar que las rectas no se cortan.
Planteo el sistema. Y la solución no debe ser S.C.D
Parte b)
No me doy cuenta como hallar ese plano.
Creo entender que entender que el producto escalar entre la normal del plano y un vector director la recta r, debería ser cero. Para que la recta y el plano sean paralelos.
Pero no me doy cuenta como hallarlo.
Desde ya muchas gracias.
Saludos.
Hola Pablo,
En la parte a, el sistema tiene que ser incompatible. Si el sistema es compatible, hay solución, la solución puede ser un punto (s.c.d) o o las rectas pueden ser coincidentes (s.c.i)
En la parte b, si las rectas no se cortan, hay dos opciones, se cruzan o son paralelas. Para ver si son paralelas, hay que ver si los vectores directores de r y s, son paralelos. En ese caso, cualquier plano que contenga a s y no contenga a r te sirve.
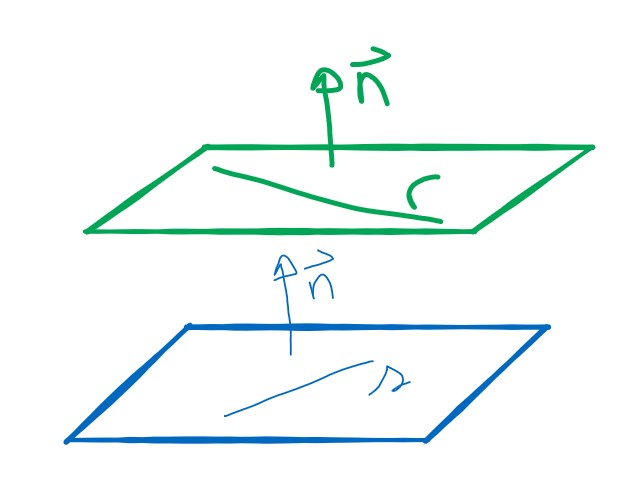
La otra opción es que se crucen, eso es lo que intento dibujar en la imagen. Si dos rectas se cruzan, quiere decir que están en planos paralelos, lo que pide el ejercicio es que encuentres el plano que contiene a s, pero ambos planos tienen la misma normal.
Las rectas que están en un plano, son perpendiculares al vector normal de plano. Entonces la normal de cualquiera de los planos, se puede obtener como el producto vectorial de los vectores directores de r y s.
Con el vector director y cualquier punto de la recta s, encontras el plano que pide el ejercicio.
Bettina.
Perfecto. Gracias