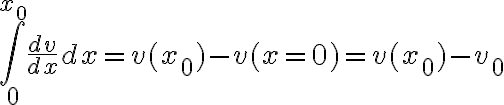ejercicio 11

ejercicio 11

de Juan Manuel Costa Fernandez -
Número de respuestas: 3

Hola ! 

En la parte C de este ejercicio tengo que hallar la velocidad en función de la posición V(x) .

Adjunto lo que intenté para resolverlo , mi pregunta es ;

¿Estoy manipulando correctamente los diferenciales ?

Luego , sobre el Vo que sumé al final : lo sumé para que tenga el sentido físico que buscamos , pero,

¿en realidad el Vo representa la constante de integración C que se obtiene de la integral de la izquierda no? 

osea 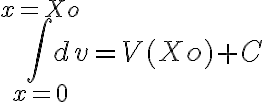 \int_{x=0}^{x=Xo} dv = V(Xo)+C siendo C = la velocidad inicial = Vo , y siendo V(Xo) la velocidad para un Xo genérico

Agradezco si me guían acerca de si estoy errado o en lo correcto.

Gracias !
Adjunto WhatsApp Image 2020-04-26 at 13.03.22.jpeg
En respuesta a Juan Manuel Costa Fernandez

Re: ejercicio 11

de Daniel Gau -

Qué tal Juan Manuel?


Tu razonamiento es correcto, y el resultado también lo es salvo que te olvidaste de pasar la masa dividiendo en el último paso.

En cuanto a la constante que te quedó, y que por lo que veo la agregaste a mano, esto no era necesario. Dicha constante viene solamente de resolver:

\int_{0}^{x_0}{dv \over dx} dx = v(x_0)-v(x=0)=v(x_0)-v_0


Espero que esto resuelva tus dudas.


Muy buen trabajo!
En respuesta a Daniel Gau

Re: ejercicio 11

de Juan Manuel Costa Fernandez -

Ahh claro , excelente , muchas gracias !!

PD: en una eventual evalucación , en una eventual evaluación , la utilización de la ley de faraday será válida ? ¿ sumaría todos los puntos que le correspondiesen al ejercicio ?