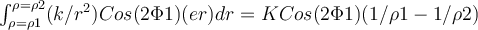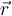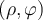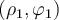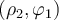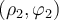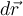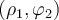Hola Juan Manuel,
una fuerza es conservativa si es posicional (depende sólo de 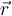 ) y el trabajo hecho por esta fuerza sobre cualquier trayectoria cerrada es cero (equivalentemente, el trabajo sobre una trayectoria que une dos puntos arbitrarios no depende de la trayectoria seguida, pero quedémonos con la primer forma para seguir la prueba).
) y el trabajo hecho por esta fuerza sobre cualquier trayectoria cerrada es cero (equivalentemente, el trabajo sobre una trayectoria que une dos puntos arbitrarios no depende de la trayectoria seguida, pero quedémonos con la primer forma para seguir la prueba).
Razonando por el absurdo, si para cierta trayectoria cerrada el trabajo no te da cero, la fuerza entonces no puede ser conservativa.
Para completar tu prueba te faltaría entonces tomar un punto inicial sobre la trayectoria sugerida (en coordenadas polares 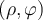 tomás por ejemplo como punto
tomás por ejemplo como punto 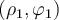 ) y calcular el trabajo de la fuerza completando una vuelta en sentido horario digamos, a la curva; este trabajo lo podés calcular a tramos: la primer integral (tramo recto de
) y calcular el trabajo de la fuerza completando una vuelta en sentido horario digamos, a la curva; este trabajo lo podés calcular a tramos: la primer integral (tramo recto de 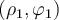 a
a 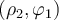 ) para evaluar el trabajo es la que decís vos, en la segunda (tramo curvo de
) para evaluar el trabajo es la que decís vos, en la segunda (tramo curvo de 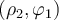 a
a 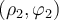 ) la fuerza es perpendicular al desplazamiento
) la fuerza es perpendicular al desplazamiento 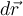 en todos los puntos (idem cuarta), mientras que la tercera (tramo recto de
en todos los puntos (idem cuarta), mientras que la tercera (tramo recto de 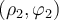 a
a 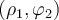 ) no se anula con la primera por la dependencia que bien observás tiene con el ángulo
) no se anula con la primera por la dependencia que bien observás tiene con el ángulo 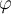 . Finalmente, te da un trabajo no nulo y por lo tanto no es conservativa la fuerza.
. Finalmente, te da un trabajo no nulo y por lo tanto no es conservativa la fuerza.
Saludos,
Ariel.
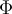 marca que :
marca que :