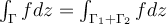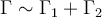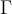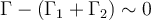pr 6 ej 1 homologia

pr 6 ej 1 homologia

de Matias Sebastian Bugna Miranda -
Número de respuestas: 3
Buenas, no me queda muy claro como aplicar el concepto de homologia.

En este ejercicio tomando 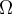\Omega como C - {a,b}

llegué a que \frac{1}{b-a} ( \int _ \Gamma \frac{dz}{z-a} - \int _ \Gamma \frac{dz}{z-b})

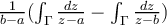
esos integrandos son holomorfos en \Omega

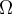
la curva \Gamma \sim \Gamma _1 + \Gamma _2
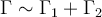
que son dos curvas que encierran al punto a y b respectivamente.

me sale que la integral de mas arriba es cero usando la dificion de indice .
que queda (2. \pi. i - 2. \pi. i) = 0

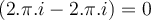
pero no se como sacarlo usando homologia y cauchy global

agradezco alguna ayuda,
En respuesta a Matias Sebastian Bugna Miranda

Re: pr 6 ej 1 homologia

de Bruno Yemini -
ahi estás, justamente, usando homología y cauchy global.

Cauchy global que dice que \int_{\Gamma} fdz = \int_{\Gamma_1 + \Gamma_2} fdz si f es holomorfa y \Gamma \sim \Gamma_1 + \Gamma_2. Entonces, basta hacer el cálculo que hiciste para probar que la integral en \Gamma es lo que planteás.
En respuesta a Bruno Yemini

Re: pr 6 ej 1 homologia

de Matias Sebastian Bugna Miranda -
pero Cauchy global no se refiere a ciclos homologicos a cero?
eso es lo que me confunde,

en este caso la homologia a cero no se da como \Gamma - (\Gamma _1 + \Gamma _2) \sim 0 ?