Buenas, no me queda claro tanto en este ejercicio como en la clase 14 de teórico por qué en la descarga del capacitor el potencial del mismo es negativo. Gracias.
En realidad el potencial es positivo o negativo dependiendo de la dirección en que recorras el circuito. Esto se debe porque cuando decimos "potencial" estamos refiriéndonos en realidad a la diferencia de potencial, entonces uno se pregunta si al pasar de un punto a otro el potencial está aumentando o dismunuyendo.
En el caso del capacitor (independientemente si se carga o se descarga), el capacitor tiene una placa con carga +Q positiva y otra con -Q. El campo que se forma en el medio del capacitor va desde la placa con carga positiva a la placa con carga negativa. Pero el potencial siempre disminuye en sentido del campo, es decir que en un capacitor la placa de carga positiva siempre está a mayor potencial que la placa de carga negativa.
Entonces si la malla es recorrida (esto es elección del que resuelve el ejercicio) atravesando primero la placa positiva y luego la placa negativa, el potencial disminuyó y por eso en la solución del ej 6, se escribió -Q/C.
Es muy importante acordarse que esa carga Q es la carga almacenada en las placas del capacitor. Ahora nos debemos preguntar cómo se relaciona esa Q con la corriente que circula, esto es diferente para carga o descarga.
O sea que si yo recorriese la malla en el sentido opuesto, el potencial aumentaría y tendría Q/C, pero cómo me doy cuenta de que la diferencia de potencial del resistor también debe cambiar su signo, o sea cómo se en que sentido va la corriente para saber si estoy recorriendo mi malla de tal modo que el resistor me causa un aumento o disminución de potencial
Hola,
si por ejemplo recorres el circuito en sentido opuesto, todos los signos van a cambiar.
Para asegurarte que están bien, te recomiendo pensar elemento a elemento. Ya viste el caso del capacitor. Para una batería el borne positivo (palito largo) está a mayor potencial que el negativo (palito corto), por lo tanto si recorres la malla del extremo negativo a positivo, el potencial aumenta. En una resistencia por la que pasa una corriente i, con el mismo sentido en el que recorres la malla, el potencial del extremos por "donde sale i" está a menor potencial que el extremo por el que "entra i", es decir el potencial disminuye.
El principal punto es que tenés que ser consistente. Si por ejemplo, mantienes el signo que le asociaste a la corriente i, pero recorres la malla en sentido opuesto, el signo del cambio de potencial en la batería y en la resistencia van a cambiar.
Con estas reglas, el sentido con el que elegiste la corriente al principio va a estar bien si la corriente que encontraste es positiva, o va a estar al revés si la corriente que encontraste es negativa.
Espero ayude. Te recomendaría elegir el circuito más sencillo que puedas pensar, elegir un sentido de la corriente, recorrer la malla y convencerte que pasa si recorres la malla en sentido opuesto (vas a encontrar la misma corriente) o si cambias la corriente de sentido (vas a encontrar que la corriente cambia de signo). De esta forma vas a poder ver que si entendés cómo cambia el potencial, la elección de como recorrer la malla o cómo elegir la corriente no es tan relevante.
Espero esto ayude. Cualquier cosa a las órdenes.
Saludos
¿Qué tal?
Aún no me queda claro por qué en la descarga de un capacitor la expresión de la ley de mallas queda:
(1) R•i + q/C = 0 con igual signo.
Una vez aislado el circuito de la batería, ¿el sentido de la intensidad del circuito no queda impuesto por el sentido de descarga del capacitor? De esta manera:
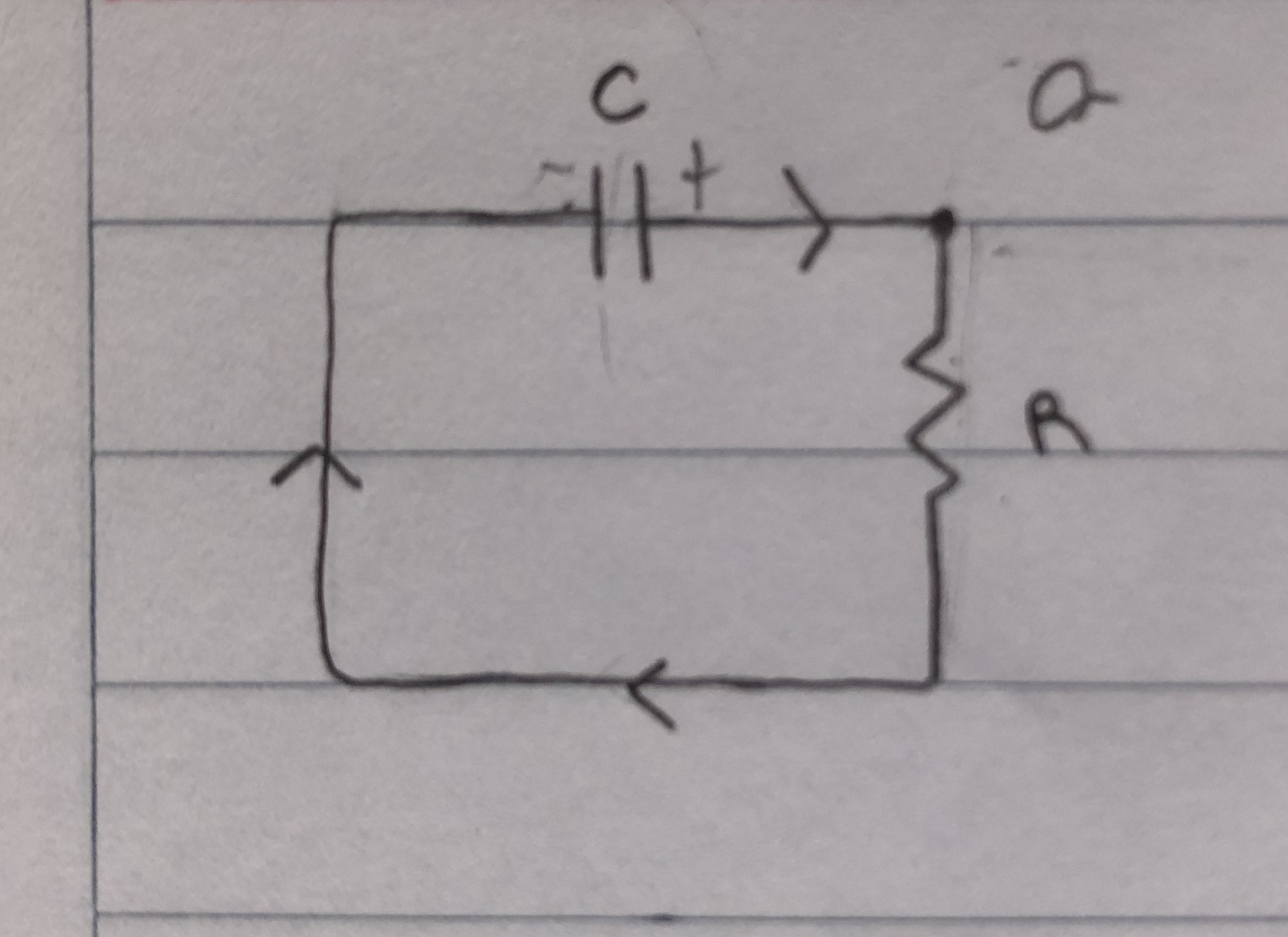
¿Por lo que entonces la ley de mallas no quedaría:
- R•i + q/C = 0 (2) ?
Si a partir de esta ecuación hallo la expresión para q(t) llego a que el exponente de e es “t/RC” en vez de “-t/RC”. Que no tiene sentido porque sabemos que q(t) debería disminuir con el tiempo.
Si me quedo con la expresión (1), llego a que el signo de la intensidad es negativo, y le damos el sentido de que se descarga en sentido contrario.
Cuando voy a sustituir i en (1) me queda el primer término negativo y el segundo positivo.
Pero si partimos de que se descarga en sentido contrario, planteando la ecuación (2), llego a expresiones erróneas.
No entiendo por qué la ecuación (2) estaría mal planteada, más allá de que llego a expresiones que no tienen sentido, al final partiendo de la ecuación (1) llego a que el término R•i en realidad tenía que se negativo.
Hola,
voy a sumir que la corriente i recorre la malla en sentido horario, estás recorriendo la malla en ese sentido y las placas del capacitor están cargadas como lo indicaste. Esa parece ser la flecha que dibujaste. En ese caso, aplicando Kirchhoff quedaría
q/C-Ri=0
El primer signo se debe el capacitor se recorre desde la placa negativa a la positiva, por lo que el potencial aumenta. el segundo signo es porque estar recorriendo la resistencia en el sentido de la corriente, y el potencial disminuye cuando recorres la resistencia en ese sentido. Eso se parece a tu Eq 2, por lo que estoy de acuerdo que debería ser la ec 2 para tu convención de sentidos en la malla y la corriente.
Pero, en este caso la corriente que dibujaste está descargando al capacitor, por lo que i=-dq/dt.
Entendamos este signo. Si la corriente es positiva (esto quiere decir que respeta el sentido que dibujaste), el capacitor pierde carga. Si la corriente es negativa, el capacitor se cargará.
Con estos signos vas a encontrar que la carga efectivamente disminuye. La solución de crecimiento exponencial no tiene sentido en este caso ya que diverge.
Espero quede más claro. Cualquier cosa a las órdenes.
Quedó muy claro. ¡Les agradezco!