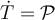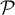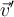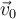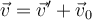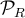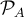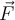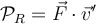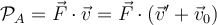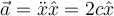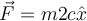Hola,
(edité el Asunto de tu mensaje porque te referís al ejercicio 4 del práctico III)
No hay ninguna razón para esperar que las cantidades medidas en un sistema deban ser iguales a las del otro a pesar de que son inerciales los dos.
En cualquiera de ellos, se verifica el Teorema del Trabajo y la Energía:
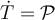 ,
,
donde  es la energía cinética que se corresponde con la velocidad observada en el sistema y
es la energía cinética que se corresponde con la velocidad observada en el sistema y 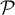 la potencia de todos los agentes que actúan sobre la partícula (que a su vez depende de la velocidad de la partícula también).
la potencia de todos los agentes que actúan sobre la partícula (que a su vez depende de la velocidad de la partícula también).
Sin embargo, la velocidad en uno y otro sistema es diferente y por lo tanto,  . Si
. Si 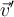 es la velocidad vista desde la nave y a su vez
es la velocidad vista desde la nave y a su vez 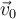 la velocidad de la nave vista desde la Tierra, tenemos que la velocidad de la partícula vista desde la Tierra es
la velocidad de la nave vista desde la Tierra, tenemos que la velocidad de la partícula vista desde la Tierra es 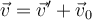 y el cuadrado de cada una no es necesariamente igual al de la otra.
y el cuadrado de cada una no es necesariamente igual al de la otra.
Acerca de la potencia podemos ver qué pasa si calculamos la potencia relativa 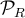 o la absoluta
o la absoluta 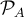 directamente a partir de la fuerza resultante
directamente a partir de la fuerza resultante 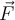 sobre la partícula:
sobre la partícula:
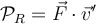
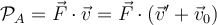
La fuerza neta en uno y otro caso es la misma (la fuerzas no cambian vistas desde un sistema inercial u otro y la aceleración de la partícula no cambia vista desde un sistema inercial con respecto a otro) por lo que la diferencia en los resultados es reflejo de la proyección de la fuerza resultante según la velocidad de la nave.
Espero que te haya aclarado un poco el panorama,
saludos,
Ariel.