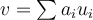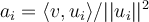Hola buen dia.
En este ejercicio desarrolle lo que esta igualado por hipotesis a <v,w> y llegue a que era igual a Σ(ai.bi.||ui||²) lo cual tendria que ser igual a Σ(ai.bi) ya que Σ(ai.bi)= <v,w> porque v y w son ortogonales.
Pero entonces llego a que ||ui||² = 1 para todo i = 1,...,n lo cual no puedo asegurar a menos que {u1,...,un} sea base ortonormal y en la hipotesis solo afirma que sea ortogonal.
¿Me podrian decir que estoy haciendo mal? O explicarme como seguir.
Gracias!