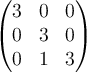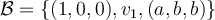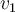GAL2-1S: Sobre ejercicio 5.2

Hoy en la clase no llegamos a ver este ejercicio y quedamos en que yo lo veía y contestaba por acá.

Un estudiante planteó que tenía problemas para hallar la base de Jordan porque el sistema le quedaba incompatible. Eso sucede si se usa uno de los vectores propios que tiene la forma (0,1,1).

Lo que se puede hacer es usar otro vector genérico de la forma (a,b,b) y ver para qué valores de a y b el sistema queda compatible. Y resolver el sistema con esos valores

Observen que cualquier vector con esta forma y el (1,0,0) determinan una base para el subespacio propio S_3.

Espero que este comentario sea de ayuda.

Saludos

Re: Sobre ejercicio 5.2

de Victoria Belen Martinez Lema - domingo, 5 de abril de 2020, 03:31

Hola, hice exactamente eso, sin embargo no puedo llegar a una forma de Jordan correcta, ¿cómo quedaría? Terminó dándome así: 1er fila: 3 0 1

2da fila: 0 3 0

3era fila: 0 0 3

Re: Sobre ejercicio 5.2

de Annabella Zapattini - miércoles, 8 de abril de 2020, 18:13

Hola Victoria.

La idea es que primero escribas la forma de Jordan y luego halles la base.

Como el subespacio propio del 3 (que es el único vap) es 2, la matriz de Jordan te queda:

$\left(\begin{matrix}3&0&0\\0&3&0\\0&1&3\end{matrix}\right)$

y tu base será $\mathcal{B}=\left\{(1,0,0),v_1,(a,b,b)\right\}$

A partir de ahí armás tu sistema para hallar $v_1$ , pero primero tendrás que elegir los valores de $a$ y $b$ para que el sistema te quede compatible.

Saludos