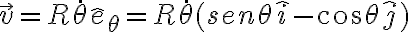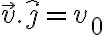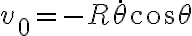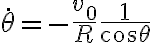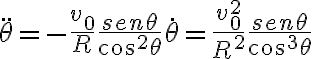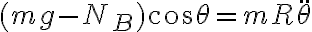Foro Práctico II

Hola, por lo que veo, tenes un error el la descomposición de la velocidad. Definiendo un versor 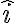$\hat{i}$ horizontal hacia la derecha y un versor 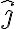$\hat{j}$ vertical hacia arriba, puede escribirse la velocidad como:

$\vec{v}=R\dot{\theta}\hat{e}_{\theta}=R\dot{\theta}(sen\theta\hat{i}-cos\theta\hat{j})$

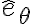$\hat{e}_{\theta}$ fue definido hacia abajo pues el ángulo $\theta$ crece hacia abajo. Pude definirse diferente pero varios  signos de menos surgirán al tomar las derivadas de  la velocidad y la aceleración. Ojo

Además la letra dice que: $\vec{v}.\hat{j}=v_0$

Entonces: $v_0=-R\dot{\theta}cos\theta$

Despejando llegamos a :$\dot{\theta}=-\frac{v_0}{R}\frac{1}{cos\theta}$

(La velocidad angular será negativa, tiene sentido pues el ángulo fue definido creciendo hacia abajo)

luego derivas: $\ddot{\theta}=-\frac{v_0}{R}\frac{sen\theta}{cos^2\theta}\dot{\theta}=\frac{v_0^2}{R^2}\frac{sen\theta}{cos^3\theta}$

Ahora planteamos Newton en la dirección de 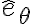$\hat{e}_{\theta}$:

$(mg-N_B)cos\theta=mR\ddot{\theta}$

(recordar que 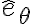$\hat{e}_{\theta}$ apunta hacia abajo)

Finalmente se sustituye y despeja la fuerza $N_B$.

Espero que se entienda, buena parte de la dificultad está en los sistemas de referencia. La derivada de un versor apunta en la dirección en que crece el ángulo. Por eso si 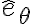$\hat{e}_{\theta}$ se define hacia arriba, al derivar 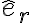$\hat{e}_{r}$ se obtiene $-\hat{e}_{\theta}$.

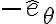Saludos, Enzo.