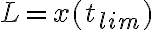Ejercicio 3 - parte c

Ejercicio 3 - parte c

de Leandro Jair Machado Da Silva -
Número de respuestas: 5

Hola. Usando 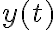y(t) hallado en la parte b, planteo 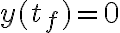y(t_f) = 0 para hallar el tiempo que tarda en caer al suelo para así luego sustituirlo en 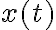x(t) y hallar L; pero me encuentro con la ecuación 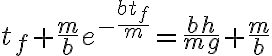t_f + \frac{m}{b}e^{ -\frac{b t_f}{m}} = \frac{bh}{mg} + \frac{m}{b} , creo que es imposible despejar 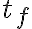t_f de ahí. Hay que suponer que 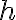h es lo suficientemente grande para así poder aproximar  e^{ -\frac{b t_f}{m}} \approx 0 ?
En respuesta a Leandro Jair Machado Da Silva

Re: Ejercicio 3 - parte c

de Ariel Fernández -

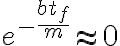Hola,

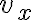no es necesario resolver la ecuación que planteás ya que de la parte a) podés obtener el tiempo t_{lim} tal que v_x cayó en un 90% de su valor inicial o lo que es equivalente, que 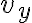v_y alcanzó el 90% de su valor límite. De ese tiempo en adelante, el movimiento es prácticamente vertical. 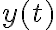Tenés que asegurarte de que una vez transcurrido t_{lim} la carga todavía no haya tocado el suelo (ya tenés hallado y(t) por lo que es sólo evaluar) y eso te da una mínima altura de vuelo (si arrancás más alto, se alcanza también el límite); además, tenés que haber recorrido en ese tiempo una distancia L en la horizontal (de t_{lim} en adelante no se modifica prácticamente x).

Saludos,

Ariel.
En respuesta a Ariel Fernández

Re: Ejercicio 3 - parte c

de Emilia Fuentefria Marchesi -

Y en la parte d, donde h es mayor que la altura mínima que calculé anteriormente. Sé que el tiempo que demora en llegar la carga al suelo es mayor que ese tiempo límite. 

Pero, cómo calculo el tiempo exacto en el que toca el suelo? 
Tendría que despejarlo de la misma ecuación de la pregunta original y no puedo.

En respuesta a Emilia Fuentefria Marchesi

Re: Ejercicio 3 - parte c

de Enzo Spera -

Hola, la expresión que obtenés no te permite hallar analíticamente el tiempo exacto. Pero a partir de los resultados de las partes anteriores podés aproximarlo.

Sabiendo cuanto le falta por caer luego de alcanzar la velocidad límite y sabiendo que desde ahí cae a velocidad constante podes determinar el tempo aproximado de vuelo. Con eso hallás la distancia x.


Saludos, Enzo.