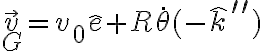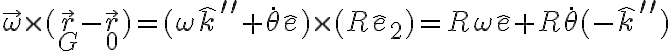Foro Práctico I

En realidad simplemente hay que usar adición de velocidades angulares como hiciste vos:

EDITO: El 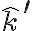$\hat{k}^\prime$ en la velocidad angular total tiene que ser 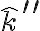$\hat{k}^{\prime\prime}$, el que sigue el vuelco.

Ahora, con respecto a tu duda, no es incoherente. Se sigue cumpliendo rodadura sin deslizar pero ahora tanto la velocidad angular como la velocidad del centro de la moneda se modifican debido al giro. Usando los versores de la figura:

$\vec{v}_G = v_0 \hat{e} + R \dot{\theta} (-\hat{k}^{\prime \prime})$

Por otro lado:

$\vec{\omega} \times (\vec{r}_G - \vec{r}_0 ) = (\omega \hat{k}^{\prime\prime} + \dot{\theta} \hat{e}) \times (R \hat{e}_2) = R \omega \hat{e} + R \dot{\theta} (-\hat{k}^{\prime\prime})$

 El vuelco no cambia nada a la relación $R\omega = v_O$, esta sigue siendo suficiente para que haya rodadura sin deslizar.