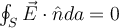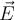Buenas,
Haciendo el ejercicio 7 del práctico nos surgió una duda y no sabemos cuál de las dos opciones es la correcta.
Cuando utilizo Gauss para despejar el campo eléctrico de la ecuación de flujo, el E que calculo es:
- el generado por la carga encerrada en los puntos de mi superficie
- el E total en los puntos de la superficie (contemplando lo que sucede fuera de ella)
Muchas gracias
Buenas! El campo eléctrico que aparece en la ley de Gauss es siempre el campo total, como en el ejercicio 1 donde no hay carga encerrada pero al plantear 
usamos el 
total que muestra la figura.
¡Hola!
Me sumo a la discusión.
En la resolución del ejercicio 7, primero encierra en un cilindro una superficie A de una de las placas y aplica Gauss para hallar el E que genera esa placa en los distintos puntos de las dos superficies del cilindro.
El E que despeja de la ecuación de flujo y de la Ley de Gauss es el E generado por la placa. Por eso es que después aplica superposición de campos eléctricos y le suma el E que genera la otra placa, hallado de la misma manera que para la primera placa.
Si el E que despejo para la primera placa fuera el total en las superficies del cilindro, no estaría teniendo en cuenta el E generado por la segunda placa.
No entiendo por qué es que entonces el E despejado de encerrar en una superficie cilíndrica una de las placas sería el E total en los puntos de las superficies del cilindro.
La ley de Gauss siempre es con el campo total, lo que pasa es que acá no la estamos aplicando directamente a la situación en la que hay dos placas. Espero que haya quedado más claro pero si no lo seguimos discutiendo!