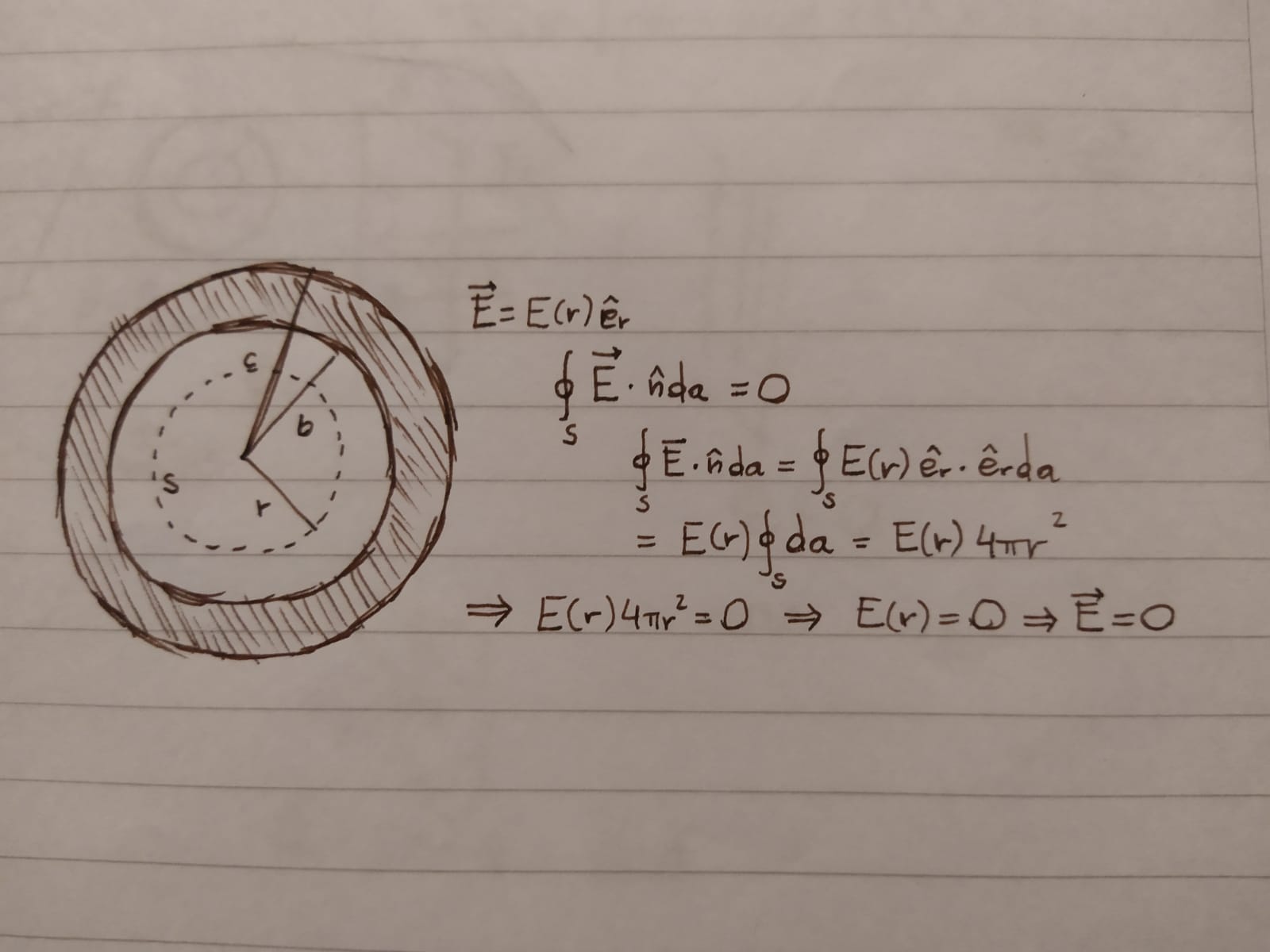Hola Leandro,
te sugiero que ir por partes tratando de justificar lo que planteas.
¿Es correcto pensar que debido al signo opuesto de las cargas, la carga de la esfera hueca va a estar toda en la cara interna, y la carga en la cara externa es 0?
Tratá de justificarlo a partir de lo aprendido sobre el campo eléctrico dentro de conductores. Por ejemplo, que superficies gaussianas elegirías para calcular el flujo eléctrico y que carga encierran esas superficies? Cómo decís vos y Nicolás, si hay una carga adentro la distribución de cargas va a ser distinta.
Otra duda: también se habla en openfing de hallar el campo "justo afuera" del conductor, ¿cómo hago para calcularlo en cualquier punto del exterior? Supongo que con ley de Gauss simplemente, pregunto por las dudas.
Ahí va la bocha. El ejemplo de Openfing es el campo muy cerca del conductor, de forma que puedes pensar que todo el resto de la superficie del conductor está muy lejos. Podés pensar que localmente la superficie es un pequeño plano. Por ejemplo, imaginate que tenes una esfera metálica de 1m de radio, el cálculo que hace Nicolás es válido muy cerca de la superficie, digamos a 1mm de ella. Pero a 2m del centro el campo va a ser totalmente distinto.
Te sugiero que trates de pensar cómo puedes hallar el campo en cualquier punto del espacio yendo sobre los ejemplos de Ley de Gauss que se discuten en el teórico y en los otros ejercicios prácticos. Creo que por lo que venís diciendo vas bien encaminado.
Si aplico Gauss para a<r<b estoy hallando el campo en ese punto pero no aparece ninguna dependencia con la esfera hueca, como que no influye en esos puntos del medio, ¿esto es así?
Es un muy buen punto. Por qué te parece que pasa esto? Como algo curioso, te recomiendo que busques info sobre la Jaula de Faraday. Te dejo un videito (en inglés), pero que me pareció de lo mejorcito.
https://www.youtube.com/watch?v=QU0fLnucE6A
Tratá de avanzar sobre el problema y si te trancas preguntá de nuevo y podemos ir a algo puntual.