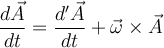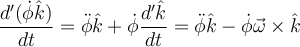Foro Práctico I

Hola. En esta hoja se calcula la derivada de la velocidad angular por dos caminos.

Primero, partiendo de la expresión 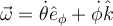$\vec \omega = \dot \theta \hat e_\phi + \dot \phi \hat k$. Esto se logra aplicando las reglas de derivación para producto y usando las derivadas de los versores conocidas. Por ejemplo, se usa 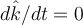$d\hat k / dt = 0$ (es un vector de la base del sistema absoluto), etc. Este método es útil cuando, precisamente, se saben hallar estas derivadas por separado. Corresponde al punto de vista del observador absoluto del ejemplo (el que usa coord. cartesianas).

Luego se calcula la misma derivada, pero esta vez aplicando la ecuación que relaciona las derivadas absoluta y relativa (ecuación 1.35 de las notas del curso) y sus consecuencias:

$\displaystyle \frac {d\vec A}{dt} = \frac{d'\vec A}{dt} + \vec \omega \times \vec A$

Entre otras cosas, se puede demostrar que la derivada relativa de la velocidad angular coincide con la derivada absoluta, 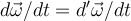$d \vec \omega / dt = d' \vec \omega / dt$ (¿podrías demostrarlo en un renglón?). Entonces, si calculamos la derivada relativa de 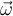$\vec \omega$ tenemos que llegar al mismo resultado.

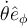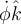Viéndonos en el sistema relativo, los vectores de la base de coordenadas esféricas están fijos pero los de la base cartesiana no. Nuevamente usamos la regla de derivada del producto para los términos $\dot \theta \hat e_\phi$ y $\dot \phi \hat k$. Para este último, por ejemplo, queda:

$\displaystyle \frac {d' (\dot \phi\hat k)}{dt} = \ddot \phi \hat k + \dot \phi \frac {d'\hat k}{dt} = \ddot \phi \hat k - \dot \phi \vec \omega \times \hat k$

Queda como ejercicio demostrar el último paso usando otra vez la ecuación 1.35. Por último, sustituyendo la expresión de 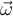$\vec \omega$ se puede calcular el producto vectorial y llegar al mismo resultado que la vez anterior.

En las notas de Ricardo Marotti hay un elemento adicional interesante: la elección de cuál es el sistema absoluto y cuál es el relativo es arbitraria, y por lo tanto se pueden intercambiar los papeles en la ecuación 1.35. Pero un detalle importante: hay que usar la velocidad angular del sistema al que le estamos llamando relativo, vista por el sistema absoluto. A la velocidad angular del sistema cartesiano con respecto al sistema esférico se le llama 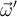$\vec \omega'$ en las notas, y es la opuesta de la velocidad angular que teníamos antes. Si creían que demostrar esto último iba a quedar como ejercicio, tenían razón.

Espero haber podido arrojar algo de luz sobre el tema. No dudes en preguntar todas las veces que sea necesario.

Saludos,

NC