Buenas
En la parte b del ejercicio si aplico la ley de Gauss para una esfera de radio r con a < r < b me queda que el campo en un punto a esa distancia es el campo producido solo por la esfera interior de carga total +q. ¿Por qué el campo producido por -q no afecta? Sé que lo preguntaron antes pero el video que adjuntaron no me aclaro mucho la duda.
Gracias
Hola Lorenzo,
Hay que tener bien presente que la Ley de Gauss refiere al flujo de campo, y no directamente al campo.
Recordemos que se puede definir el flujo como el número de líneas de campo que atraviesan una superficie.
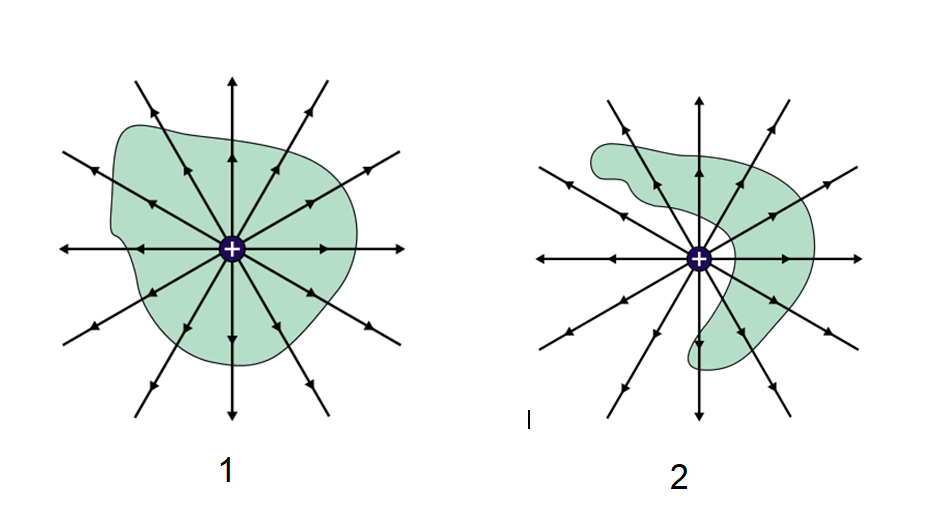
Analicemos el caso más simple de todos, el de la carga puntual, cuyo campo es bien conocido. En ambas fotos encontramos la misma situación, la carga puntual con su campo radial.
En el caso 1, la superficie encierra la carga. Tenemos 12 líneas que atraviesan la superficie. Ahora fijate que a esa superficie le podés dar la forma que se te ocurra sin que el número de líneas se modifique. Siempre el número de líneas es 12 (salientes).
En particular, si justo elegís una esfera centrada en q, la integral de flujo queda muy sencilla, y en ese caso es posible calcular el campo mediante la ley de gauss. Pero esto sólo se da en casos de simetría, como los ejercicios que estamos realizando en el repartido.
Vamos a la figura 2. Allí elegimos una superficie que deja afuera la carga. Fijate que el campo en todo el espacio es el mismo que anteriormente, porque es la misma situación que en la fig.1. Lo único diferente es la elección de la superficie imaginaria.
Sin embargo, con esta elección, el flujo que atraviesa esta superficie ya no es el mismo, porque el número de líneas que entran, es el mismo que las que salen. El flujo es cero, mientras que el campo no lo es.
¿Qué quiero decir con todo esto?
Que el flujo sea cero a través de la superficie gaussiana, no quiere decir que el campo sea cero. Si la carga está en el exterior, sigue produciendo el campo que ya conocemos, pero no aporta flujo neto que atraviese la superficie.
La ley de gauss nos habla del flujo. Nosotros la aprovechamos para calcular el campo en los casos con cierta simetría en los que podamos resolver la integral sobre la superficie gaussiana.
¿Se entiende?
Gracias por tu respuesta. Entiendo que el flujo por una superficie cerrada sea cero no implica que el campo sea nulo. Pero mirando la solución subida del ejercicio, noto que llegan a la misma respuesta que yo y es de donde surge mi duda: ¿Por qué es solo el campo producido por la esfera interna el que aparece y no también el producido por la esfera grande de carga -q?
Lorenzo,
te propongo que hagas el siguiente ejercicio.
Como sabemos, aquí vale el Principio de superposición, ¿verdad?
Entonces hagamos esto. Resolvé el mismo problema pero en 3 pasos.
1) Si sólo existera el cilindro interior (sin el tubo)
2) Si sólo existera el tubo exterior (sin el cilindro)
3) Aplicá el Principio de superposición (suma de los campos anteriores) para calcular el campo en el espacio entre ellos.
A ver si así se ve mejor porque sucede eso en este caso.
Saludos!