Buenas! Si te referís al ejercicio 9b, ese ejercicio no habla de conductores. Así que asumiendo que era el 3b:
Como decís, el campo que produciría sólo la esfera de radio a es el mismo que para a<r<b en el caso de las dos esferas. También es verdad que si consideramos sólo la esfera hueca y tomamos cualquier superficie cerrada adentro, la carga encerrada es 0 y por lo tanto el flujo es 0.
Para calcular el campo lo importante es recordar que este problema sigue teniendo simetría esférica, y por eso el campo va a ser radial y sólo va a depender de la distancia r al centro de la esfera hueca. Entonces para calcular el campo a una distancia r, tomamos como superficie gaussiana una esfera de radio r<b. El módulo del campo es constante sobre esa esfera y entonces sale de la integral. En el dibujo vemos cómo es el cálculo:
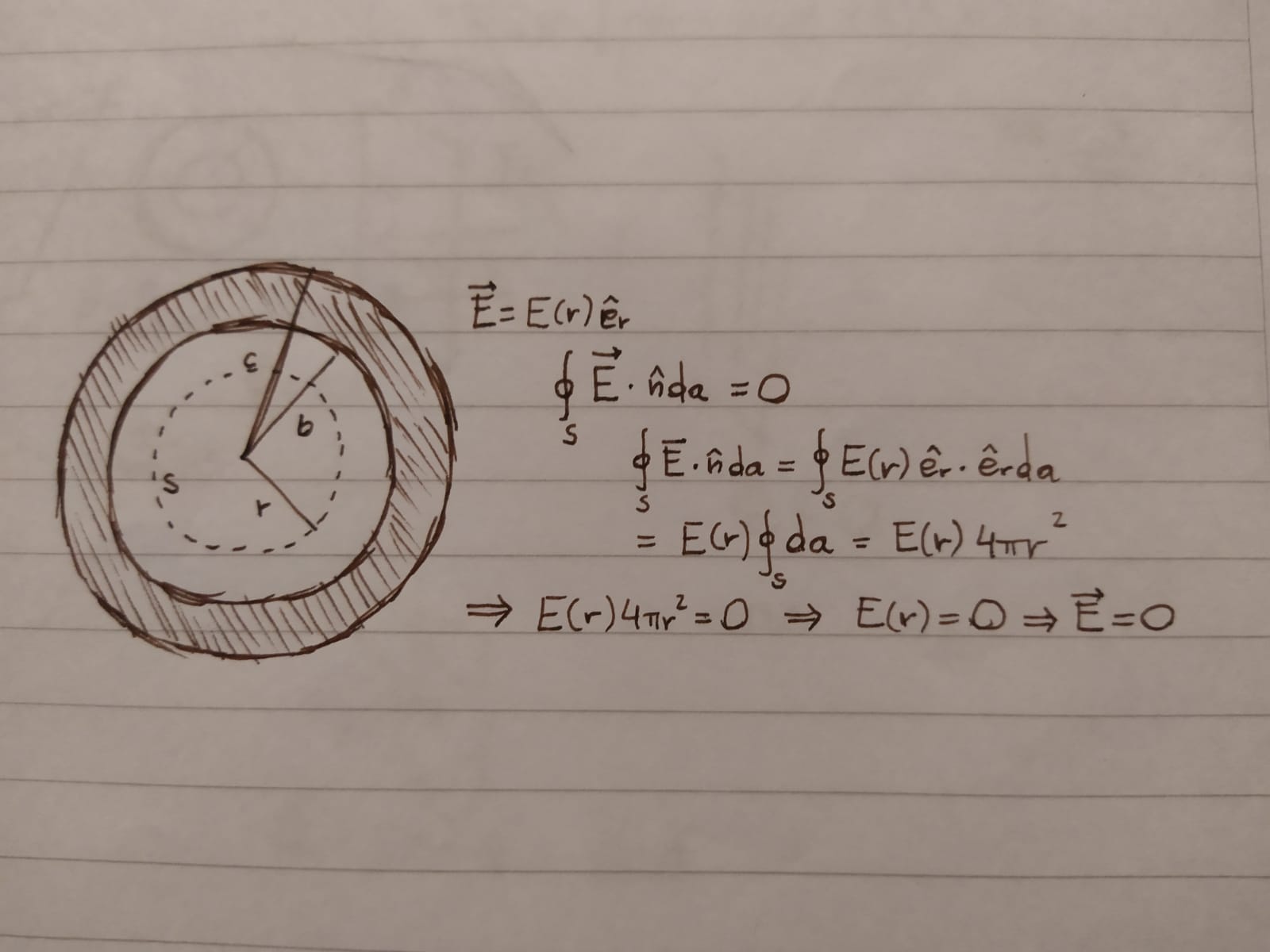
La conclusión entonces es que el campo que genera la esfera hueca es 0 en el hueco, por eso el campo total en a<r<b en el problema de las dos esferas es igual al campo generado por la esfera de radio a.
Y por último un comentario respecto a la jaula de Faraday: Acá lo que vimos recién es que el campo en el hueco de una esfera hueca conductora es 0 si no tiene carga adentro, usando un argumento de simetría para decir que el campo es radial. Sin embargo vale en general que el campo eléctrico en el hueco de un conductor es 0 si no hay carga dentro del hueco. Esto es independiente de la forma del conductor y de la forma del hueco, y es lo que observamos en el video de la jaula de Faraday. Es una propiedad muy interesante, pero (hasta donde yo sé) no podemos demostarla con las herramientas matemáticas que usamos en este curso.
